Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método de Ponchon – Savarit – Colunas com seções intermediárias

Ver Todos os Exercícios

Teoria

Importância

Até agora, vimos sobre o conceito do Método Ponchon-Savarit. No entanto, só vimos esse método para colunas de destilação com duas seções (Absorção e Esgotamento). No entanto, o método de Ponchon Savarrit pode ser aplicado para outros tipos de coluna, como, por exemplo, colunas com seção intermediária. E é isso que vamos ver nesse tópico, beleza?

Nós vamos ver como exemplo uma coluna com duas cargas. No entanto, não importa o tipo de coluna que aparecer na questão, você precisa sempre seguir o mesmo procedimento. Define suas envoltórias, faz os balanços de energia e depois disso tenta encontrar todos os pontos que são colineares.... Bora lá ver isso na prática 😊

Método Ponchon – Savarit com colunas com seção intermediária

Nós vimos que é possível, pelo Método Mc-Cabe Thiele, avaliarmos coluna com duas cargas e aí, entre essas cargas, temos uma seção intermediária.

Bora fazer o balanço de energia dessa envoltória 1?

V n H n - L n - 1 h n - 1 = D   h d + q c

V n H n - L n - 1 h n - 1 = D h d + Q c = ∆ D

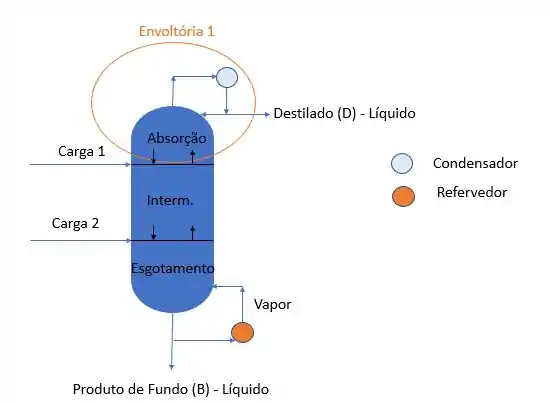
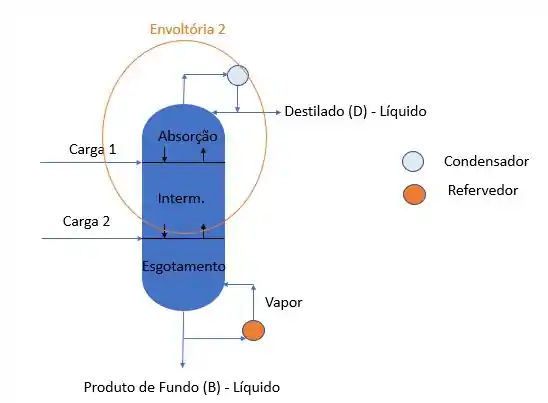
Já para o balanço de energia na envoltória 2, obtemos que:

V j H j = L j - 1 h j - 1 + D h d + q c - F 1 h f 1

V j H j - L j - 1 h j - 1 = D h d + Q c - F 1 h f 1

V j H j - L j - 1 h j - 1 = ∆ D - F 1 h f 1

E aí, podemos definir que ∆ D - F 1 h f 1 = ∆ ' , então, esses já seriam 3 pontos colineares no diagrama de entalpia e composição. Logo, V j H j - L j - 1 h j - 1 = ∆ ' seriam outros 3 pontos colineares, pois:

V j H j - L j - 1 h j - 1 = ∆ D - F 1 h f 1 = ∆ '

Se a gente fizer o Balanço de energia na coluna inteira ( Balanço Global), temos que:

F 1 h f 1 + F 2 h f 2 = D h d + B h b + q c - q r

Nesse caso, como temos duas cargas, podemos utilizar uma dica que demos na parte de Mc-Cabe Thiele e definir que:

F 1 + F 2 = F -

z f = ( F 1 z f 1 + F 2 z f 2 ) F -

Substituindo isso no Balanço de Energia da coluna, temos que:

F - h f = D h d + B h b + q c - q r

Reorganizando, temos que:

F - h f = ∆ D + ∆ B

E esses vão ser os três pontos colineares do nosso balanço global!

Podemos também definir outros pontos colineares a partir da seguinte equação:

F 2 h f 2 = ∆ D - F 1 h f 1 + ∆ B

Como definimos que ∆ D - F 1 h f 1 = ∆ ' , então F 2 h f 2 = ∆ ' + ∆ B e aí teremos em cada uma das equações 3 pontos colineares.

Aplicação dos Pontos colineares no gráfico

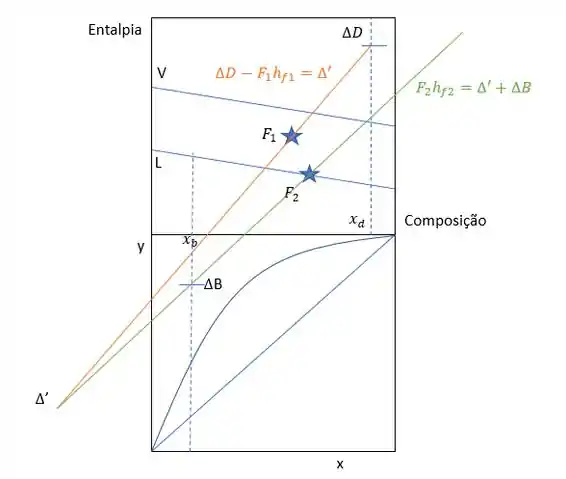
Agora que já fizemos todas as relações possíveis e já sabemos quais pontos são colineares, vamos supor que temos uma coluna com condensador e refervedor totais com duas cargas ( carga 1 é parcialmente vaporizada e carga 2 é líquida saturada), e vamos marcar esses pontos no gráfico!

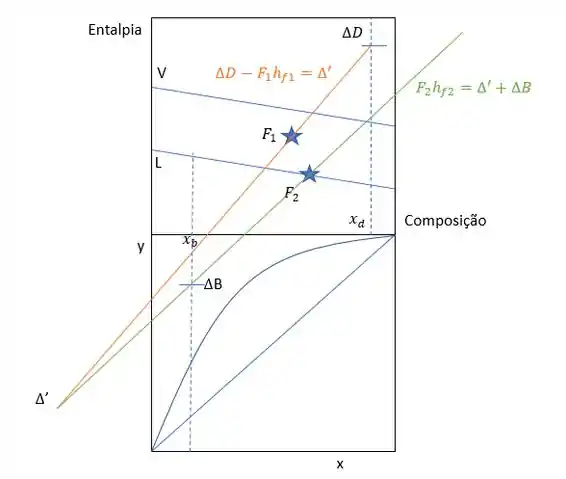
Além disso, nós aproveitamos também na figura acima e traçamos as retas com os pontos possíveis que eram colineares. Agora, vamos marcar a reta de balanço global. A reta de Balanço Global vai ligar e delta B e delta D e vai passar pelo ponto z f que foi calculado de acordo com as informações de cada uma das cargas, de acordo com os pontos colineares definidos por essa equação: F - h f = ∆ D + ∆ B .

A primeira coisa que temos que fazer é traçar uma reta ligando F 1 e F 2 e marcar nela o nosso ponto z f . Depois disso, a reta global vai passar pelo ∆ D ,   ∆ B e o F - .

Para traçar os estágios nessa coluna, vai ser muito parecido com o que vimos para colunas de apenas duas seções. No entanto, quando estivermos na região entre reta laranja e a reta verde ( ou seja, entre absorção e esgotamento), vamos usar o ∆ ' para a reta de operação ( que é o ∆ ' da seção intermediária). Para a seção de absorção e de esgotamento, vai continuar exatamente do jeito que conversamos, beleza?

E só para te lembrar que se cair outro tipo de coluna na sua prova não se despera! Faz os balanços de energia e defina pontos colineares! Essa é a grande sacada do Método Ponchon-Savarit. Bora ver algumas delas lá nos exercícios?!?

Aplicação dos Pontos colineares no gráfico

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

O número de cargas da coluna interfere no método de resolução de problemas de colunas com seções intermediárias?

Passo 1

Não, o método de resolução não muda. Nós vamos sempre definir as envoltórias da coluna, fazer os balanços de energia e depois encontrar todos os pontos que são colineares.

Resposta

O método de resolução não muda.

Exercício Resolvido #2

Origem do exercício

Trace a reta global da coluna com condensador e refervedor totais com duas cargas, sendo a carga 1 parcialmente vaporizada e a carga 2 líquida saturada.

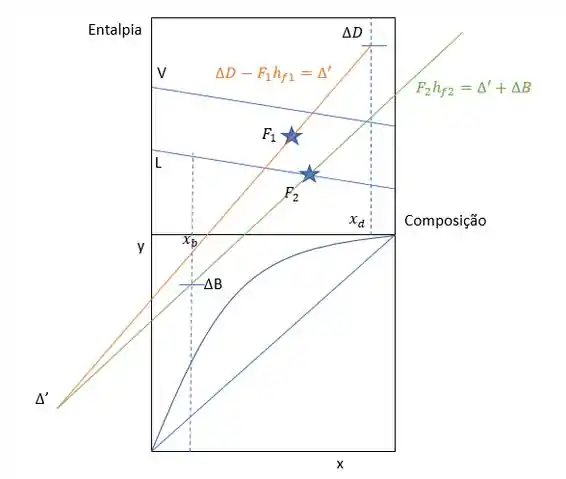
Passo 1

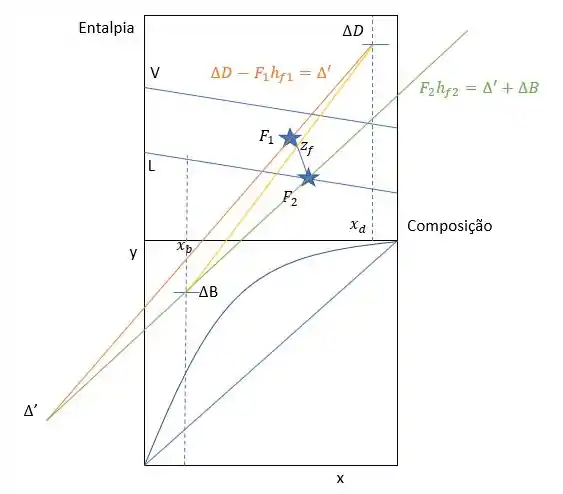
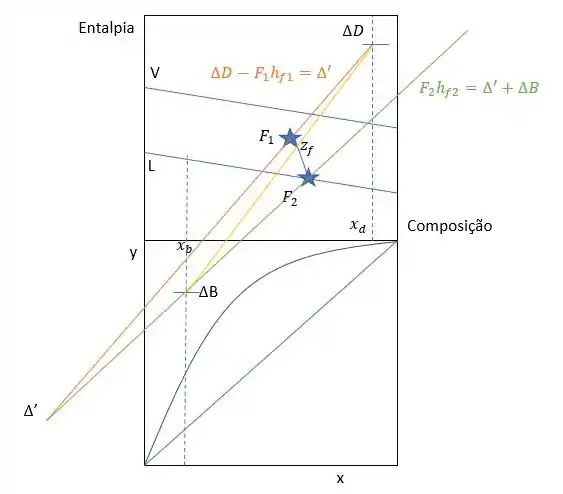
Para marcar a reta de balanço global, vamos ligar delta B e delta D e vai passar pelo ponto z f , que já está marcado no gráfico.

Passo 2

Unindo ∆ B   com ∆ D temos,

Resposta

Exercício Resolvido #3

Elaboração própria

Calcule o número de estágios da coluna com condensador e refervedor totais com duas cargas, sendo a carga 1 parcialmente vaporizada e a carga 2 líquida saturada.

Passo 1

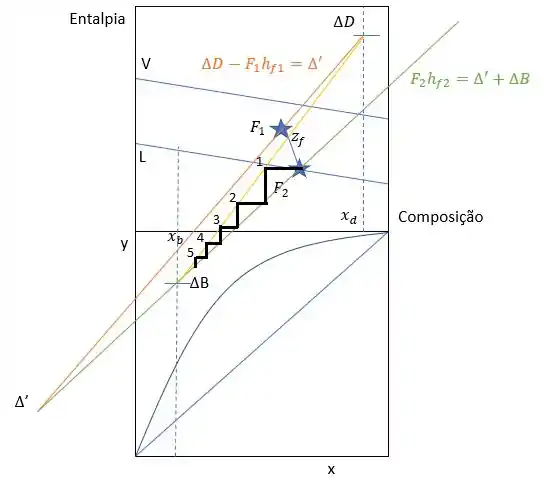
Vamos encontrar os estágios traçando os degruas, no qual suas pontas vão bater na reta global (em amarelo). E vai começar no encontro de z f com F 2 indo até ∆ B .

Passo 2

Seguindo o caminho descrito, temos um total de 5 estágios.

Resposta

5 estágios.

Exercício Resolvido #4

Elaboração própria

Faça o balanço de energia do envoltório 1 da coluna com seção intermediária.

Passo 1

Para fazer o balanço de energia nós precisamos seguir a famosa regrinha:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos lá!

Passo 2

Aplicando a regra nesse caso, temos:

V n H n - D   h d - q c = L n - 1 h n - 1

Reescrevendo isso de outra forma,

V n H n - L n - 1 h n - 1 = D h d + Q c = ∆ D

Resposta

V n H n - L n - 1 h n - 1 = D h d + Q c = ∆ D

Exercício Resolvido #5

Elaboração própria

Faça o balanço de energia do envoltório 2 da coluna com seção intermediária.

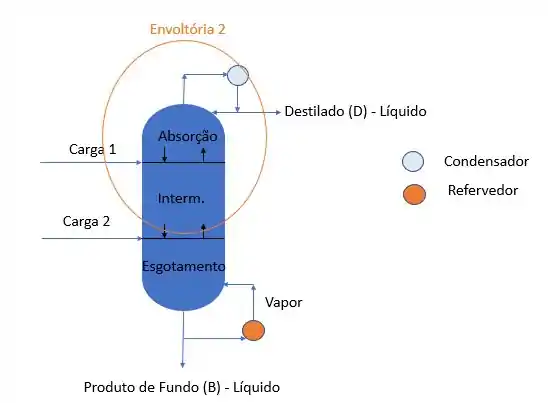
Passo 1

Para fazer o balanço de energia nós precisamos seguir a famosa regrinha:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos lá!

Passo 2

Aplicando a regra, obtemos:

V j H j - D h d - q c = L j - 1 h j - 1 - F 1 h f 1

Reescrevendo e arrumando essa expressão temos,

V j H j - L j - 1 h j - 1 = D h d + Q c - F 1 h f 1

V j H j - L j - 1 h j - 1 = ∆ D - F 1 h f 1

Onde,

∆ D = D h d + Q c

Resposta

V j H j - L j - 1 h j - 1 = ∆ D - F 1 h f 1

Exercício Resolvido #6

Elaboração própria

Faça o balanço de energia global da coluna com seção intermediária.

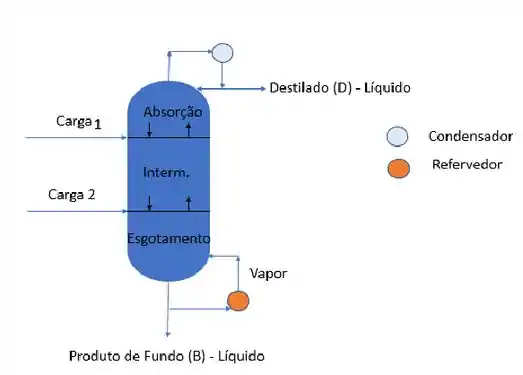
Passo 1

Para fazer o balanço de energia nós precisamos seguir a famosa regrinha:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos lá!

Passo 2

Aplicando a regra temos que:

F 1 h f 1 + F 2 h f 2 - D h d - B h b - q c + q r = 0

Reorganizando,

F 1 h f 1 + F 2 h f 2 = D h d + B h b + q c - q r

Passo 3

Nesse caso, como temos duas cargas, podemos utilizar uma dica que demos na parte de Mc-Cabe Thiele e definir que:

F 1 + F 2 = F -

z f = ( F 1 z f 1 + F 2 z f 2 ) F -

Substituindo isso no Balanço de Energia da coluna, temos que:

F - h f = D h d + B h b + q c - q r

Reorganizando, temos, por fim:

F - h f = ∆ D + ∆ B

Resposta

F - h f = ∆ D + ∆ B

Exercício Resolvido #7

Elaboração própria

Calcule o valor de Q c sabendo que a variação do destilado é 1200   K J / m o l e que h D = 10   K J / m o l .

Passo 1

Faaaaala aiii, tudo bem?? Nessa questão nós queremos encontrar o valor de Q c . Mas antes vamos analisar o que o enunciado nos deu. Nós temos:

F 1 = 220   K J / m o l

F 2 = 300   K J / m o l  

D = 100   K J / m o l

h D = 10   K J / m o l

Δ D = 1200   K J / m o l

Então já dá para desconfiar que vamos precisar usar o balanço de energia, beleza? Então simbora!

Passo 2

Do balanço de energia do primeiro envoltório nós vimos que:

V n H n - L n - 1 h n - 1 = D   h d + q c

V n H n - L n - 1 h n - 1 = D h d + Q c = ∆ D

Então,

∆ D = D h d + Q c

Passo 3

Agora precisamos substituir os valores que temos para encontrar Q c :

1200   K J / m o l = 100   K J / m o l 50   K J / m o l + Q c

Ou seja,

Q c = 2   K J / m o l

Resposta

Q c = 2   K J / m o l

Exercício Resolvido #8

Elaboração própria

Calcule o valor de h f sabendo que a variação do fundo é 1 0 00   K J / m o l . Dados: h D = 10   K J / m o l , ∆ B = 17 0   K J / m o l , Q c = 3 K J / m o l .

Passo 1

Oi oi oieee, tudo bem?? Nessa questão nós queremos encontrar o valor de h f . Mas antes vamos analisar o que o enunciado nos deu. Nós temos:

F 1 = 220   K J / m o l

F 2 = 300   K J / m o l  

D = 100   K J / m o l

h D = 10   K J / m o l

Δ B = 1 7 0   K J / m o l

Q c = 30   K J / m o l

Com isso em mente vamos precisar de duas equaçõezinhas:

Δ D = D h d + Q c

F - h f = ∆ D + ∆ B

Passo 2

Vamos começar usando a primeira equação do passo anterior, substituindo as informações dadas:

Δ D = D h d + Q c

Δ D = 100 K J / m o l 10 K J / m o l + 3 K J / m o l

Δ D = 1300   K J / m o l

Agora já podemos ir para a próxima equação.

Passo 3

Na segunda equação do Passo 1 temos que:

F - h f = ∆ D + ∆ B

Mas ainda não calculamos o valor desse F - que é nada mais, nada menos que a soma da corrente das duas cargas, ou seja,

F - = F 1 + F 2

F - = 220   K J / m o l + 300   K J / m o l

F - = 520   K J / m o l

Passo 4

Agora sim podemos substituir os valores na equação e encontrar quem queríamos desde o começo, h f ,

520 K J m o l × h f = 1300   K J / m o l + 170   K J / m o l

h f = 2,8   K J / m o l

Fimm!! \o/

Resposta

h f = 2,8   K J / m o l