Diagrama de Equilíbrio
Teoria
Diagrama de Equilíbrio
Até agora vimos diagramas de fases, normalmente com composição no eixo x e temperatura no eixo y. Agora chegou a hora de aprender a, usando os diagramas vistos até agora, construir um tipo diferente de diagrama: o diagrama de equilíbrio.
O diagrama de equilíbrio é diferente porque, embora não seja fixa, a temperatura não aparece explicitamente nele. E ele é suuuuper importante na disciplina de operações unitárias, principalmente pra quando falamos de destilação. Então, é beeem importante entender como construímos ele, certo?
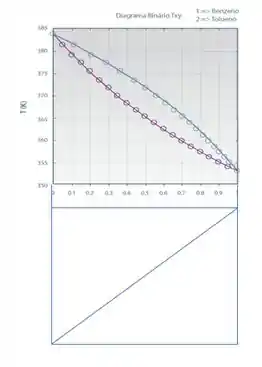
Pra chegarmos nesse diagrama, precisamos seguir algumas etapas, que estão representadas nas figuras a seguir, beleza?
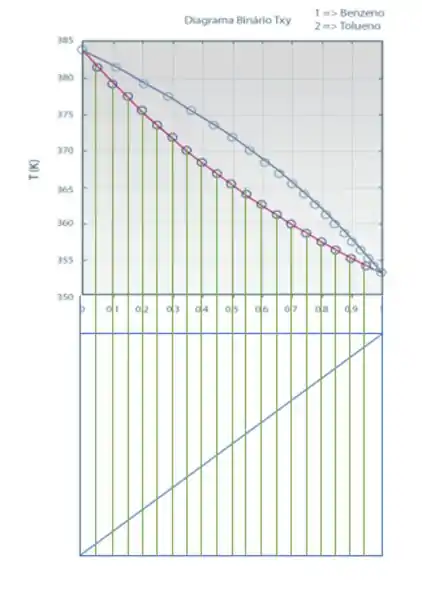
- Construir um quadro logo abaixo do diagrama que possuímos. O novo quadro deve ter a mesma largura que o quadro superior e precisamos traçar sua diagonal.
- O eixo horizontal do gráfico que já possuímos representará a fração molar na fase líquida no novo gráfico. Portanto, todos os pontos da curva de líquidos deve ser marcado no novo gráfico construído, tipo como estamos mostrando com as linhas em verde, ok?
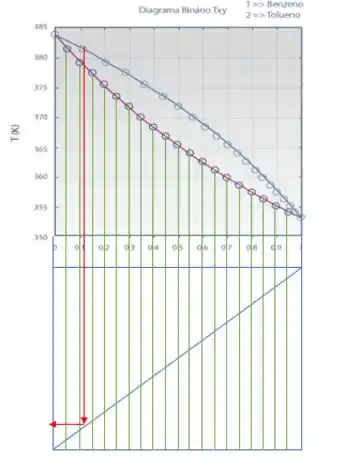
- Para os pontos da curva de vapor, que vão representar nosso , eles estarão no eixo vertical do gráfico de baixo. E para colocar esses pontos lá, vamos fazer o seguinte. Vamos descer eles até a diagonal (pois nesse ponto ), e aí vamos rebater ele para o eixo vertical, beleza? É o procedimento que estamos marcando em vermelho!
- Vamos fazer isso para todos os pontos da curva de vapor. Só que, repara que, nesse primeiro ponto, a linha do e (primeira linha horizontal e primeira linha vertical) em equilíbrio se encontraram. E é justamente esse ponto que vamos precisar marcar!
- Para fechar, quanto terminamos de fazer isso em todos os pontos e ligarmos as estrelas, vamos obter o seguinte Diagrama de Equilíbrio.
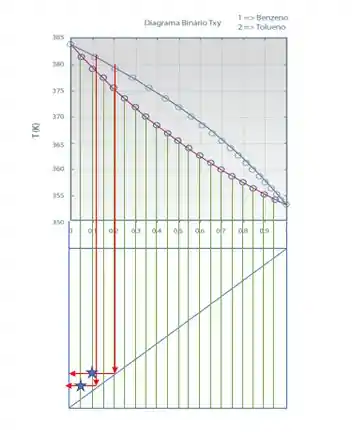
Aí no nosso exemplo marquei com uma estrela o encontro da primeira linha vertical com a primeira linha horizontal, e fiz mais um pontinho como exemplo, beleza? E aí temos que repetir isso para todos os pontos e marcar os encontros.
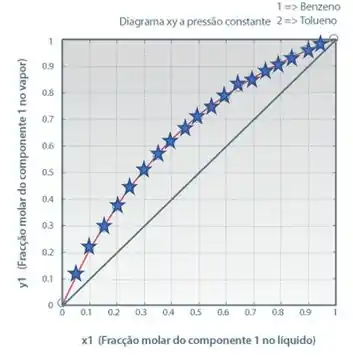
Lembrete: é o Diagrama que vamos usar na destilação!
Cálculo do Diagrama de Equilíbrio
Vamos supor que a gente não tenha o outro diagrama, será que é possível calcular esses pontos?
SIMMMMMM e dá para fazer isso a partir de um conceito que já conhecemos: a volatilidade relativa.
Como só temos dois componentes em cada fase, podemos dizer que e também. Então, substituindo, na equação da volatilidade relativa, obtemos que:
Que podemos reorganizar da seguinte forma:
Então, se a gente conhecer a volatilidade relativa, é so chutar vários valores de , que vamos obter E aí conseguimos traçar a curva.
Bora ver um exemplo em que a volatilidade relativa seja constante e igual a 2,5. Então, nossa fórmula fica:
Agora podemos variar o valor de de 0 até 1, de 0,1 em 0,1 e calcular o
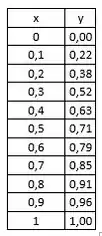
E, a partir daí, podemos plotar esses dados e obter o nosso sonhado diagrama:
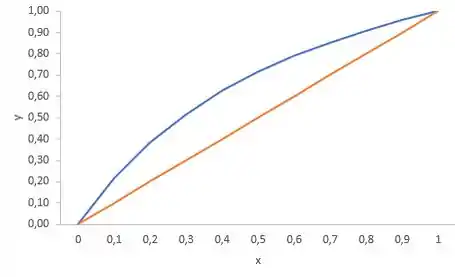
LEMBRETE IMPORTANTE: Tem que traçar a diagonal (linha laranja).
Cálculo do Diagrama de Equilíbrio
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Determine o diagrama de equilíbrio de um sistema contendo dois compostos, sabendo que a volatilidade relativa () é constante e igual a 2.
Passo 1
Vamos relembrar o que é volatilidade relativa?
E sabemos também que a soma dos dois componentes em cada fase tem que somar um! Logo, e . Então, bora escrever tudo em função de um componente só:
Podemos simplificar e escrever em função de .
Passo 2
Já temos a volatilidade relativa e vamos escolher vários valores de variando de até . Esses valores são arbitrários, mas só para facilitar vamos fazer variando de em .
Passo 3
Agora, vamos substituir todos os valores de na fórmula para acharmos os respectivos .
E aí bora ver os resultados:
Vou colocar a conta para o como exemplo, beleza?
E aí, se repetimos isso para todos os pontos, chegamos naquela tabela.
Passo 4
A próxima etapa é colocarmos esses pontos no gráfico!
Mas para finalizar o diagrama de equilíbrio, precisamos colocar a diagonal marcando os pontos . No gráfico abaixo, marquei a diagonal de laranja. Então ele agora tá completinho, beleza?
Resposta
Exercício Resolvido #2
Elaboração própria.
A partir do diagrama de equilíbrio apresentado a seguir, determine a volatilidade relativa () entre os compostos envolvidos, sabendo que a volatilidade é constante.
Passo 1
Primeiríssssima coisa que precisamos fazer é lembrar o que é volatilidade relativa, beleza?
E sabemos também que a soma dos dois componentes em cada fase tem que somar um! Logo, e . Então, bora escrever tudo em função de um componente só:
Passo 2
Precisamos calcular a volatilidade, né? Então vamos pegar um ponto do gráfico e substituir na fórmula.
Peguei um bem tranquilo para ler. O e o , então vai ser esse ponto que vamos usar.
Passo 3
Vamos substituir os pontos que achamos?
Achamos uma volatilidade de !!
Repara que como foi dito para considerar a volatilidade constante, foi possível escolher qualquer ponto, mas nem sempre é assim.
Resposta
2,25
Exercício Resolvido #3
Elaboração própria.
Marque Verdadeiro ou Falso sobre a obtenção dos diagramas XY:
a. Os eixos x e y devem ser escritos em função da fração molar do mesmo componente.
b. Volatilidades relativas maiores resultam em curva xy e diagonais mais próximas, facilitando o processo de separação.
Passo 1
Bem, a letra a. indica que os eixos devem ser escritos em função da fração molar do mesmo componente. E isso tá corretinho, pois já estamos falando de fases diferentes ( e ). Para estudarmos o equilíbrio entre elas, é essenciaaalll que estejamos falando das frações do mesmo componente, beleza?
Então, essa afirmativa é verdadeira.
Passo 2
Na segunda afirmativa, as coisas já ficam um pouquinho mais confusas... Eu sei! Mas vamos com calma.
Primeira informação é que volatilidade relativa maior resulta em curvas mais próximas da diagonal. Isso é totalmente FAKE! Quando a gente tem volatilidade relativa alta, isso indica que as tendências daqueles compostos em estar na fase líquida e vapor são bem diferentes entre si. Logo, seus e serão super diferentes!
Então, como essa curva pode estar perto da diagonal, se a diagonal representa justamente quando ? Não pode né? Então é falso!
Resposta
a. Verdadeira
b. Falso
Exercício Resolvido #4
Elaboração própria.
Uma empresa precisava optar entre trabalhar com o Sistema A ou Sistema B, seus diagramas de equilíbrio estão disponíveis a seguir. Esses dois sistemas eram compostos por dois componentes e esses componentes precisam ser separados pela ação da temperatura. Para qual sistema essa separação será mais facilmente realizada?
Passo 1
O que temos de dados são os diagramas versus . Nós sabemos que esse diagrama é função da volatilidade relativa, certo?
Quanto mais afastada a linha azul estiver da diagonal, isso indica que temos um valor de muito maior que . Se esses valores são tão distintos assim, possuímos volatilidades relativas maiores (). Dá para vermos isso pela fórmula:
Então, podemos concluir que: quanto mais afastada a curva azul for da diagonal, maior é a nossa volatidade relativa. Mas e aí? O que eu faço com essa informação?
Passo 2
Aplicando essa informação nos gráficos, vemos que o sistema A tem uma volatilidade relativa bem maior que o sistema B.
Quanto maior a volatilidade relativa de um sistema, mais fácil vai ser a separação entre as fases líquida e vapor durante o aquecimento. Isso ocorre pois mais um composto vai estar presente em uma fase e menos na outra, sendo mais fácil de separá-lo!
Então, o Sistema A seria o escolhido por ser o mais fácil de realizar a separação.
Resposta
Sistema A
Exercício Resolvido #5
Elaboração própria com diagrama do Portal da Engenharia Química
Nem todos os sistemas binários, constituídos por duas substâncias, possuem volatilidade relativa constante. Um exemplo muito comum é a mistura etanol e água.
Selecione ao menos dois pontos para mostrar que a volatilidade relativa não é constante para esse sistema.
Passo 1
Nessa questão, precisamos calcular a volatilidade relativa em dois pontos e comparar para ver as diferenças.
Escolhi dois pontos para a gente ver isso, beleza?
Vamos então citar esses pontos como Ponto 1 e Ponto 2.
O Ponto 1 possui e . O Ponto 2 possui e , aproximadamente.
Passo 2
A próxima coisa que precisamos fazer é substituir esses pontos na fórmula da volatilidade.
Para o Ponto 1:
Para o Ponto 2:
Resumindo:
Passo 3
CARAMBA!
Os valores foram muiiito diferentes! E é isso mesmo, toda vez que uma mistura não for ideal ou que seus componentes não forem muito parecidos, não vamos poder considerar a volatilidade constante. Então, precisamos sempre estar muito atentos, beleza?
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração Própria
Observando o diagrama de equilíbrio líquido- vapor abaixo, pode ser afirmado que a mistura possui alfa constante?
Passo 1
A questão pergunta se o alfa é constante. Alfa é a nossa volatilidade relativa, que é dada pela seguinte equação.
Uma possibilidade para conferir isso é calcular o alfa para dois ou mais pontos do nosso diagrama e conseguir ver se o alfa é igual ou não. Caso o alfa nesse diagrama seja igual nas diferentes composições, então temos um alfa constante 😊
Passo 2
Vamos avaliar isso para três valores espaçados e calcular os alfas, ok? Vamos representar esses pontos com coração de várias cores no gráfico !
A fórmula para calcular o alfa é dada por:
Então, para o coração azul:
Para o coração verde:
E, por fim, no coração vermelho, temos que:
Os alfas são diferentes, mas as diferenças não são muito grandes, pode ser apenas desvios por conta da precisão do gráfico. Portanto, podemos dizer que o alfa é constante 😊
Resposta
Alfa é constante.