Área específica superficial
Produzido por Marcelo AlvesTeoria
Introdução
Imagina que você tá fazendo uma pesquisa num laboratório de catálise. Aí o seu orientador chega e pede pra você colocar no reator, catalisador suficiente para ter de área superficial dele.
"Tá. Mas por que ele tá interessado na área superficial?" Cara, porque a superfície do catalisador é onde ocorre a catálise de fato. A área superficial também é super importante pra outros fenômenos, tipo transferência de massa, transferência de calor, etc.
Mas bora lá. Como será que você poderia medir a área superficial do catalisador? Dá um trabalhinho, mas é possível!

Mas mais simples do que medir a área superficial é descobrir ela relacionando com massa ou volume, que são coisas bem mais fácil de se medir, né? Essas relações da área superficial são o que a gente chama área específica superficial.

Quando falamos em área específica superficial (alguns chamam de "superfície específica"), estamos falando de área superficial por unidade de alguma coisa. Vou mostrar pra você dois casos.
Área específica superficial por unidade de massa ()
A primeira que vamos ver é quando relacionamos a área superficial da partícula com a massa dela. Daí, vamos ter a área específica superficial por unidade de massa ():
Uma coisa que vale a pena falar é que se você tiver dados para um conjunto de partículas e não para uma individualmente, também pode calcular o . Daí você considera os dados do conjunto né. Tipo assim:
É, essencialmente, a mesma coisa.
Área específica superficial por unidade de volume ()
Outra que também costuma aparecer é a , que é quando relacionamos a área superficial com volume, olha só:
Da mesma forma que vimos pro , se temos dados para um conjunto de partículas:
Medição da área superficial
Tá, quando tivermos ou o , basta saber a massa ou volume, respectivamente, e vamos ter a área superficial. Mas se não tivermos nem nem , tem que medir direto a área superficial.

Vou falar de duas maneiras, ok?
- Se você tiver como saber o , que é o diâmetro da esfera de mesma área superficial que a partícula, é tranquilo, né? Você aplica a fórmula da área superficial da esfera, usando o , e pronto:
- Quando não temos informação sobre o tamanho e forma da partícula, mas sabemos que ela pode adsorver alguma substância, vamos explorar isso.
Só pra te lembrar, já vimos o lá no tópico de tamanho.
Adsorção é quando uma substância fica ligada numa superfície. Se você sabe, por exemplo, a quantidade x de um gás que fica adsorvida por de uma certa superfície, pode ir pro laboratório e fazer um experimento: ver quanto foi adsorvido numa amostra e aí fazer regra de 3 para saber qual a área superficial total na sua amostra.
E aí, bora exercitar um pouquinho?

Área específica superficial por unidade de massa ( a m )
Área específica superficial por unidade de volume ( a V )
Medição da área superficial
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Calcule a área específica superficial por unidade de massa, em , de uma amostra de cuja área superficial medida, em um experimento, foi de .
Passo 1
Bora lá! O enunciado pede pra gente calcular a área específica superficial por unidade de massa, que é o , de uma amostra de partículas. A fórmula do é:
O enunciado já nos deu tanto o numerador como o denominador:
O lance é que se pediu o com unidade . A área superficial já esta em mas precisamos converter a massa para .
Convertendo a massa ():
Daí:
Passo 2
Agora é só jogar na fórmula:
Resposta
Exercício Resolvido #2
Elaboração própria
Calcule a área específica em volume, em , sabendo que:
Passo 1
O exercício pede pra gente calcular a área específica em volume, que é o .
Como dados temos a área específica em massa,:
E temos, também, a densidade das partículas:
Passo 2
Bora olhar só pra dimensões por um momento, ok?
Quando eu falar de algo entre colchetes, estou me referindo as dimensões desse algo, tipo assim:
Então bora lá! Vamos ver as dimensões de , e :
Agora repara quais as dimensões da multiplicação de por :
Cortando com :
Que são as dimensões de !!!
Eu fiz isso pra provar pra você, através das dimensões, que:
Passo 3
Ok, vimos que é verdade:
Substituindo os valores dados:
Cortando com :
Já achamos o ,em ,mas o enunciado pede em então bora converter:
Daí:
Cortando os :
Prontinho.
Resposta
Exercício Resolvido #3
Elaboração própria
Um laboratório de catálise necessita de de área superficial de catalisador para uma certa reação. Determine a massa de catalisador necessária.
Dados:
Passo 1
Temos uma informação sobre a área superficial requerida, , e temos que calcular a massa necessária de catalisador para termos essa área.
Epa! Lembra a fórmula do :
Vamos escrever ela assim, mais simplesinha.
Tendo o é de boas relacionar área superficial e massa, né? Só temos o e a densidade das partículas, ... não nos foi dado .
Massssss, lembra que vimos lá no exercício 2 que:
Daí temos como calcular o .
Passo 2
Calculando o :
Substituindo os valores:
Dividindo e cortando os :
Passo 3
Agora que temos o , é felicidade pura haha
Substituindo os valores que temos:
Resposta
Exercício Resolvido #4
Elaboração própria
Calcule a área específica em volume de uma casca cilíndrica cujas especificações são:
Passo 1
Bora primeiro entender melhor essa geometria: casca cilíndrica é como se você tirasse um cilindro de dentro de um cilindro. Aí tem um buraco no meio. Tipo assim:
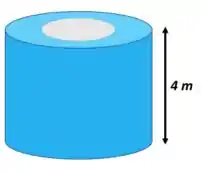
Esse buraco vai de uma ponta até a outra aí a vista superior fica assim, olha:
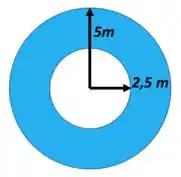
Temos que calcular a área específica em volume, :
Daí, vamos precisar calcular a área superficial e o volume dessa casca cilíndrica.
Passo 2
Bora começar calculando a área superficial.
A superfície da casca cilíndrica inclui a área lateral externa (), área lateral interna (), anel da base () e anel do topo ().
Calculando um por um:
A área lateral externa é a área lateral de um cilindro: perímetro da base multiplicada pela altura. Como o perímetro da base é uma circunferência:
Já que e :
A área lateral interna é calculada de forma semelhante, já que a lateral interna também tem forma cilíndrica:
A altura é a mesma, , mas :
A área da base é um anel; a área do anel é a área do circulo maior menos a área do circulo menor, ou seja:
Substituindo os valores:
E repara que a base é igual ao topo, daí as áreas são iguais:
Somando tudo:
E não podemos esquecer da unidade! Como trabalhamos com todos os comprimentos em metros, a unidade da área é :
Passo 3
Agora precisamos do volume dessa casca cilíndrica. A fórmula para volume é:
Já calculamos a área da base e já temos a altura: e .
Substituindo os valores:
Não esquecendo da unidade:
Passo 4
Temos e . Agora é só dividir um pelo outro e teremos o , em :
Resposta
Exercício Resolvido #5
Elaboração própria
Prove, utilizando esferas, que, para uma mesma morfologia, quanto maior o tamanho da partícula, menores os valores de e .
Passo 1
Temos que provar que quanto maior o tamanho da partícula, ou seja, quanto maior o diâmetro dela, menores vão ser e para ela. Lembrando as fórmulas deles:
O lance de “para uma mesma morfologia”, é que se você está falando, por exemplo, de um cilindro de diâmetro , quando for analisar um diâmetro , tem que pegar um cilindro também, né! Não pode começar a frase em grego e acabar em espanhol; se começar em um idioma, tem que terminar naquele mesmo idioma. Da mesma forma, se começa analisando uma forma geométrica, faz toda a sua análise com aquela forma.

Show! Vamos precisar das fórmulas de área superficial () e de volume () da esfera:
Passo 2
Bora começar pelo , porque já temos as fórmulas para área superficial e volume da esfera. Vamos escrever o para uma esfera genérica de diâmetro :
Substituindo:
Simplificando:
Ou seja, repara que o é proporcional a , isto é, ele é inversamente proporcional ao diâmetro.
E a constante de proporcionalidade (), no caso da esfera, é , já que, como já achamos:
Daí, quanto maior o diâmetro da esfera, menor o , menor a relação área superficial por volume:
Provado!
Passo 3
Já provamos o . Provar o agora é de boas. Já vimos, no exercício 2, que:
Rearranjando:
Já calculamos que pra esfera:
Substituindo:
Daí, assim como para o , o é inversamente proporcional ao diâmetro . A única coisa que muda é a constante de proporcionalidade (), que pro da esfera é:
Daí:
Provamos também : )
Resposta
Ei, a resposta está no passo a passo :)