Diâmetros Médios
Produzido por Marcelo AlvesTeoria
Introdução
Já vimos como calcular o diâmetro para uma partícula. Mas e se essa partícula resolver passear com as amigas? Teremos então uma população de partículas, certo?
Essas partículas não vão necessariamente ter o mesmo tamanho e, muitas vezes, vai nos interessar conhecer um diâmetro médio para a população. Um ponto importante é que vamos considerar, em todos os cálculos, que as partículas têm a mesma forma, ou seja, iguais fatores de forma B e C, igual esfericidade, etc; elas vão diferir apenas em tamanho.
No título desse tópico já está a dica de que tem mais de uma forma de calcular diâmetro médio. O mais importante é, sem dúvida, o diâmetro médio de Sauter, mas bora ver um por um:
Diâmetro médio de área superficial ()
A ideia aqui é calcular a área superficial total (vai contar todas as partículas) e depois, através de uma área média, calcular o .
Antes de vermos a fórmula para o , quero que você relembre que posso representar a área superficial de forma genérica com o fator de forma B:
Daí, para um conjunto de partículas e lembrando que vamos considerar que partículas têm a mesma forma:
E consideramos nessa fórmula que
Daí, dividindo tudo por B e isolando o :
Bora ver um exemplo só pra entender melhor? Imagina que tem um total de partículas sendo que têm tamanho e 3 têm tamanho . Daí:
Diamêtro médio volumétrico ()
É a mesma ideia do , mas agora vamos considerar o volume. Bora relembrar então do fator de forma C:
Daí, para o conjunto de partículas:
Dividindo tudo por C e isolando o :
Diamêtro médio de Sauter ( ou )
Esse é o mais importante de todos. Coloca uma estrelinha nele aí haha. A definição dele é:
Mas dificilmente vamos calcular por aqui.
Se a gente substituir as expressões que acabamos de achar para e nessa definição, a gente vai acabar chegando numa fórmula mais usada:
Calma que eu explico o que significa cada coisa:
Mas a soma de todas as porcentagens fecha em 100%. Que é a mesma coisa que 1, né? Daí:
Esse , que em alguns lugares pode aparecer como um , é um , se você for analisar a curva de distribuição de tamanhos.
E se você pensar em ir diminuindo cada vez mais essas subfaixas , até ficar um tamanho infinitesimal? Opa, tá parecendo quando aprendemos integral em Cálculo 1, aquela introdução com somas de Riemann. E é exatamente essa ideia: o somatório dá origem a uma integral e, como , ao diminuir muito o , vira um . Além disso, o vira apenas , já que o intervalo é infinitesimal. Daí:
E para resolver essa integral, vamos precisar escrever o em função de , usando algum modelo de distribuição de tamanhos. Dá uma olhada num exemplo:
Se aplicarmos raiz quadrada dos dois lados:
Isolando o :
E é essa expressão que jogaríamos na integral.
Pra finalizar o tópico, só uma observação: vimos 3 fórmulas de calcular o diâmetro médio de Sauter; não se assute se a questão pedir pra você calcular por mais de uma fórmula e os resultados não derem exatamente iquais, ok? Têm aproximações envolvidas nos cálculos.
Fechou. Bora pros exercícios. : )
Diamêtro médio volumétrico ( d - V o l )
Diamêtro médio de Sauter ( d - ou d 32 )
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Lista 1 Prof. Medronho, Questão 10 - Adaptado
Determinar o diâmetro médio de Sauter da seguinte areia:
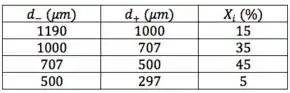
Passo 1
Vamos por partes: temos que calcular o diâmetro médio de Sauter. Dentre as informações do enunciado tem , daí, vamos ter que usar a fórmula:
Mas o que são esses e que aparecem na tabela? Bora entender isso melhor.
Resumo da ópera: esses nos dizem os limites da faixa. Daí, usamos eles pra calcular .
Outra coisa que temos que prestar atenção é que não fazemos contas com porcentagem. Bora passar logo os para base unitária:
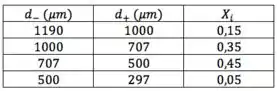
Passo 2
Para calcular o diâmetro médio de Sauter, já vimos que vamos precisar dos relativos a cada faixa. Cada é a média aritimética dos diâmetros limites da faixa . Calculando:
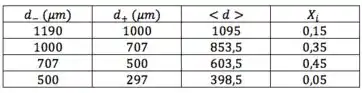
Uma vez calculados os , é com eles que vamos trabalhar; não mais vão nos interessar e . Vou até tirá-los da tabela pra não confundir:
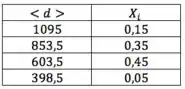
Agora é só aplicar a fórmula de :
Gosto pessoal: prefiro calcular esse sómatorio separado e depois juntar tudo. Se você preferir, pode calcular direto.
Jogando o resultado do somatório:
E trabalhamos com diâmetros em :
Resposta
Exercício Resolvido #2
UFRJ - Lista 1 Prof. Medronho, Questão 9
A peneiração de uma amostra de areia gerou a seguinte distribuição de tamanhos:

Pede-se:
- Calcular o diâmetro médio de Sauter da amostra, com base no modelo GGS.
Passo 1
Temos uma tabela com pares (), com diâmetros em , e vamos ter que calcular o diâmetro médio de Sauter com base no modelo GGS, que é um dos modelos que vimos pra descrever a curva em função de . Daí, como está envolvendo , vamos ter que usar a fórmula para diâmetro médio de Sauter que envolve também, que é essa aqui:
Vamos ter que isolar o diâmetro na equação para e lançar nessa fórmula. Mas primeiro de tudo, precisamos da equação pra . Então bora lá:
Passo 2
Temos que calcular a equação pra pelo modelo GGS, que tem a cara:
Para estimar os parâmetros e , vamos precisar dessa equação linearizada e depois fazer regressão linear, lembra? Como vimos lá no tópico “Distribuição de Tamanhos”, a forma linearizada do GGS fica:
E, comparando com a equação genérica de uma reta, :
Portanto, vamos precisar lançar, num gráfico, versus . Bora construir, então, uma tabela com os valores. Mas não esquece que os valores de precisam estar em base unitária!!!

E, também, temos que desprezar pontos com e pontos com quando vamos fazer linearizações. Daí bora sumir com esse último ponto aí logo:

Agora sim bora achar os pares ():
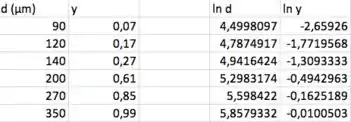
Fazendo a regressão linear com os pares ():
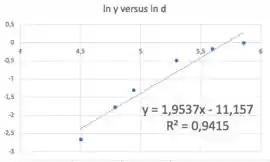
Lembrando que:
Daí:
Substituindo o valor de nessa segunda equação e cortando os “menos”:
Daí, escrevendo nossa equação de :
Passo 3
Bora agora calcular o diâmetro médio de Sauter:
Vamos precisar de , ou seja, em função de ; temos . Daí, temos que isolar o na fórmula do :
Elevando os dois lados a , isto é, :
Rearranjando:
Agora é só jogar isso na fórmula do diâmetro de Sauter:
Gosto pessoal: eu prefiro resolver a integral separado a ir levando no denominador. Acho mais fácil pra pra enxergar sei lá haha. Se preferir ir de uma vez só, de boas também.
Voltando pra fórmula do diâmetro médio:
Resposta
Exercício Resolvido #3
Elaboração própria
Dada a amostra abaixo, calcule o diâmetro médio de Sauter da amostra. Utilize o modelo Sigmóide para os seus cálculos.
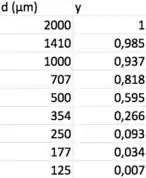
Passo 1
Nessa questão, temos que calcular o diâmetro médio de Sauter da amostra. Para isso, nos foi dada uma tabela com pares (), daí, já dá pra notar que vamos ter que usar:
Mas antes, vamos ter que encontrar a expressão de , isto é, a expressão de em função de . Depois, colocamos e aí substituímos na integral. E o enunciado pediu pra usarmos o modelo Sigmóide para achar a curva . Daí, ela vai ter essa cara:
Passo 2
Bora lá. Primeiro de tudo, temos que achar a expressão para e, para isso, vamos precisar da forma linearizada do modelo para fazer regressão linear e achar os parâmetros:
Comparando com a equação de uma reta, :
Vamos montar uma tabela com os valores de e , mas antes disso, lembre que desprezamos pontos com ou . Então corta logo esse primeiro ponto:
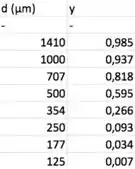
Agora sim, bora montar a tabela com e :
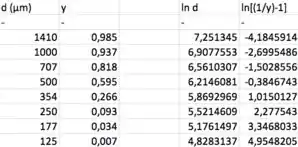
Fazendo a regressão linear de :
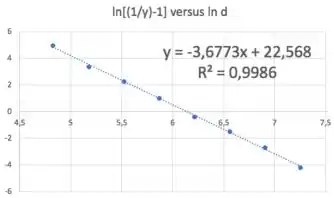
Agora podemos calcular os parâmetros do modelo Sigmóide:
Substituindo o valor de :
Daí, fica:
Passo 3
Já temos , mas precisamos de para conseguir calcular o diâmetro médio de Sauter. Daí, temos que isolar .
Invertendo os dois lados:
Jogando o para esquerda:
Elevando os dois lados a , isto é, :
Isolando e calculando :
A expressão é feia mas é essa aí haha
Passo 4
Agora é só jogar na expressão do diâmetro médio de Sauter e calcular.
Eu calculo a integral em separado, aí:
E é nessa hora que valorizamos a nossa calculadora hahah Dá pra resolver a integral na mão, mas, na prova, provavelmente o tempo vai ser corrido então aconselho ir se familiarizando com sua calculadora.
Voltando pra fórmula de :
Resposta
Exercício Resolvido #4
UFRJ - Lista 1 Prof. Medronho, Questão 11
Uma amostra, de determinado produto de moagem, apresentou a seguinte análise de peneiras:
![]()
Pede-se:
Calcular o diâmetro médio de Sauter da amostra com base em
Passo 1
Temos que calcular o diâmetro médio de Sauter de uma amostra e para isso nos foi dada uma tabela relacionando números Mesh Tyler com massas de amostra. Já extraí a informação de Mesh Tyler e transformei na informação de e , através da tabela que relaciona essas duas informações lá na teoria.
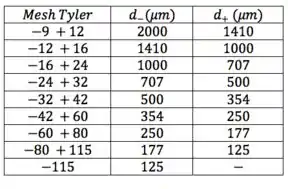
O que tem de novo nessa questão é que ela não relaciona, diretamente, as frações de massa num intervalo com os diâmetros limite do intervalo ( e ). Temos que calcular. Para isso, precisamos saber a massa total de amostra e aí pode ver qual a fração de amostra em cada intervalo.
Fora isso, é igual a fórmula que já vimos para diâmetro médio de Sauter:
Passo 2
Bora somar as massas de todos os intervalos:
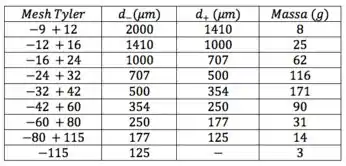
De posse da massa total, calculamos a fração de massa, ,em cada intervalo:
Pro primeiro intervalo, por exemplo:
Daí, adicionando uma coluna pros :
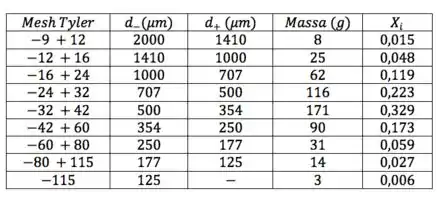
Passo 3
Vamos, também, precisar da média aritmética dos diâmetros limites de cada intervalo, isto é, . Para o primeiro intervalo, por exemplo, vai ficar:
E teremos que fazer essa conta até o penúltimo intervalo.
“Mas e o último intervalo? Só tem um dos limites do intervalo, que no caso é o , como faço?” Sempre que só tiver um dos limites, você diz que a média é ele próprio. Faz sentido: a média de um número só é ele mesmo. Daí, bora adicionar uma coluna para os :
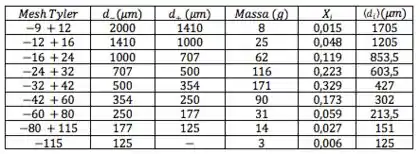
Show! Agora já temos uma relação entre e . Só eles importam agora:
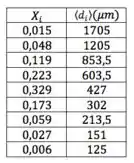
Passo 4
Agora é só jogar tudo na fórmula e calcular:
Como eu já disse, prefiro calcular o somatório separado e depois voltar pra fórmula:
Voltando pra fórmula:
Resposta
Exercício Resolvido #5
UFRJ - Lista 1 Prof. Medronho, Questão 12 - Adaptado
A análise granulométrica de uma amostra de minério de barita originário de Itaguaí-RJ é fornecida abaixo:
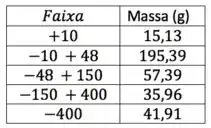
- Calcular o diâmetro médio de Sauter da amostra
Obs: As faixas estão em Mesh Tyler!
Passo 1
Da mesma forma que na questão anterior, a primeira etapa é converter as informações de Mesh Tyler para diâmetro, olhando a tabela que tem na teoria.
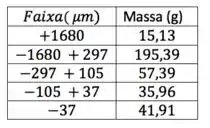
A ideia de resolução também é a mesma: temos que achar as frações mássicas em cada intervalo e a média aritmética dos diâmetros limite de cada faixa. Depois, é só jogar na fórmula de :
Os valores na tabela com estão associados com e os com associados a . NÃO TEM NADA A VER COM O DIÂMETRO SER POSITIVO OU NEGATIVO. Até porque não teria nem sentido um diâmetro negativo.
Passo 2
Vamos por etapas. Primeiro, bora calcular os , lembrando que só tiver 1 diâmetro associado a uma faixa, o dessa faixa é esse próprio diâmetro:
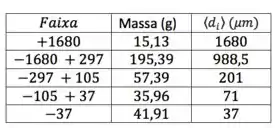
Agora, precisamos calcular os associados a cada faixa. Para isso, precisamos da massa total da amostra, já que:
Bora calcular a massa total, que é o somatório das massas de todas as faixas:
Agora podemos calcular o associado a cada faixa. Para a primeira, por exemplo, fica:
Fazendo isso para cada uma das faixas:
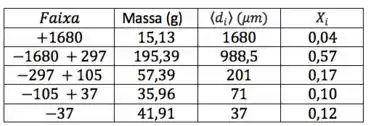
Repara que
Agora que temos os e os associados, nada mais importa:
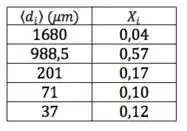
Passo 3
Agora é so jogar na fórmula e calcular o diâmetro médio de Sauter:
Eu prefiro calcular o somatório em separado e depois juntar tudo:
Juntando:
Resposta
Exercício Resolvido #6
UFRJ – Lista 1 Prof. Medronho, Questão 10
Determinar o diâmetro médio de Sauter da seguinte areia:
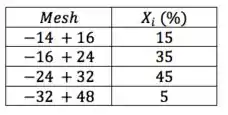
Passo 1
Essa aqui é a fórmula do diâmetro médio de Sauter:
Mas, antes de aplicar essa fórmula para resolver o problema, precisamos transformar os dados da tabela de Mesh Tyler para diâmetros!
Bora adicionar, na tabela, linhas para . Vou passar, também, os pra base unitária logo, já que não podemos trabalhar com eles em porcentagem na fórmula.
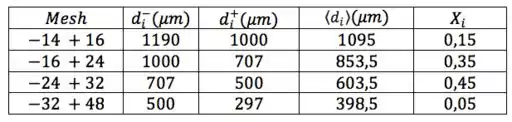
Passo 2
Para calcular o diâmetro médio de Sauter por frações parciais, só o que nos interessa são . Uma vez que os temos, podemos esquecer todo o resto.
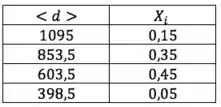
Agora é só aplicar a fórmula de :
Gosto pessoal: prefiro calcular esse sómatorio separado e depois juntar tudo. Se você preferir, pode calcular direto.
Jogando o resultado do somatório:
E trabalhamos com diâmetros em :
Resposta
Exercício Resolvido #7
UFRJ –Lista 1 Prof. Medronho, Questão 14
Deseja-se peneirar areia, , no sistema de peneiras vibratórias esquematizado. Pede-se:
- Determinar o diâmetro médio de Sauter da areia com base em
- Determinar a produção de em e o diâmetro médio de Sauter de cada uma das frações com base em
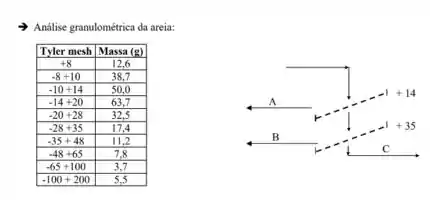
Passo 1
Nessa questão, temos uma alimentação que passa por 2 peneiras e dá origem a 3 correntes. E queremos saber a vazão e os diâmetros médios de Sauter. Então, precisamos usar também os conceitos de peneiração!
Como vamos precisar calcular diâmetros médios, vamos precisar de informação de diâmetros e, por isso, temos que converter para diâmetro. Além disso, o enunciado pede pra calcular os diâmetros médios de Sauter por , daí, vamos ter que usar a seguinte fórmula:
Bora então nos organizar. Vamos ter que adicionar a tabela: . Para a conversão de para diâmetros, temos que usar aquele tabelão que tá lá na teoria e para calcular os , temos que usar:
Então bora calcular o a massa total, :
Daí a primeira linha, por exemplo, vai ter :
Montando nossa tabela:
Dois comentários que eu queria fazer a respeito dessa tabela são:
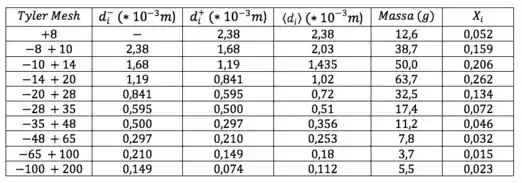
- Repara que eu coloquei, na tabela, os diâmetros em milímetro (). Fiz isso pra gente não ficar sempre só colocando diâmetros em micra (). Sei que é algo meio bobo, mas uma unidade que você nunca usou pode acabar confundindo na hora da pressa na prova
- Na hora de calcular o na primeira linha, só temos uma informação de diâmetro (relativo ao ). Não tem nenhuma outra informação sobre algum outro diâmetro para essa faixa, então usamos
Agora, bora resolver o que o enunciado pede : )
Passo 2
- Determinar o diâmetro médio de Sauter da areia com base em
- Determinar a produção de em e o diâmetro médio de Sauter de cada uma das frações com base em
É só aplicar fórmula.
Eu prefiro trabalhar com o somatório em separado e depois juntar:
Repara que eu coloquei em evidência o porque ninguém merece ficar repetindo isso vezes né? Haha Voltando pra fórmula de :
Passo 3
Vamos por etapas: primeiro calculamos as produções e depois pensamos em diâmetros médios para essas faixas, ok?
A primeira peneira é de , daí ela retém todas partículas de pra baixo, ou seja, retém as partículas de diâmetro pra cima. O que tiver diâmetro menor do que isso, passa por essa peneira de 14. Então, a corrente vai ser composta de partículas de diâmetros pra cima.
Já a peneira retém as partículas com de pra baixo, lembrando que só está indo pra essa segunda peneira o que passou pela peneira. Ou seja, a corrente vai ser composta por partículas de diâmetro entre e . E o que passa por essa peneira vai para a corrente .
Igual fizemos no exercício anterior, bora destacar na tabela, com diferentes cores, o que vai pra cada corrente, ok?

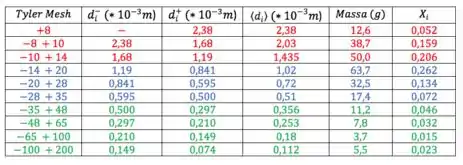
Numa prova, você não vai ter como mudar a cor da tabela, mas aconselho você destacar de alguma forma essas faixas, de boas? Circula ou faz chaves, por exemplo.
Já dividimos a tabela e sabemos quais frações vão para quais correntes. Agora é só somar as frações parciais para achar a fração total de cada corrente e multiplicar pela vazão, que é , para saber a vazão de cada uma das correntes . Assim, olha:
Daí a vazão da corrente , que vou chamar de , vai ser:
Da mesma forma, a gente calcula as vazões de :
E para :
Passo 3
Agora só falta calcular os diâmetros médios de cada uma das frações A, B e C. Vamos com atenção. Bora relembrar a forma genérica para diâmetro médio de Sauter baseado em frações parciais.
MASSSSSSSSS os que vamos usar para calcular aqui NÃO são os mesmos que estão naquele tabelão que a gente fez. Temos que considerar as frações de cada corrente. Tipo, é como se você estivesse recebendo três problemas diferentes. Bora ver o caso do que vai ficar mais claro.

Qual a massa total dessa amostra que “inventamos”?
Daí a fração relativa a massa de é:

Os são os mesmos, já que não é porque a partícula mudou de corrente que o tamanho dela muda, certo? Daí calculando o diâmetro médio de Sauter para a fração A, que vou chamar de :
Eu sei que você já sabe que eu prefiro fazer o somatório em separado, mas resolvi fazer tudo junto aqui pra não ficar mais enrolado haha
Para a corrente , é como se tivesse:

Para calcularmos os , precisamos calcular a massa total dessa amostra que inventamos:
Calculando as frações :

E o diâmetro médio para essa corrente é:
Para a corrente :

Calculando as frações :

Resposta
- ,
,
,