Distribuição de Tamanho
Teoria
Introdução
No tópico de introdução à distribuição de tamanho vimos o que é distribuição de tamanho e como interpretar essa informação. Chegamos a uma tabela de peneiração com vários diâmetros e calculamos os valores de y e z, certo?
Mas e como calculamos distribuições de tamanho contínuas?
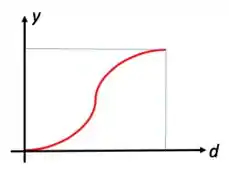
Podemos utilizar equações já existentes, que representem o comportamento do y para um certo diâmetro, a partir dos dados da tabela de peneiração.
E pra que queremos conhecer esses modelos de distribuição de tamanho? Como eles são contínuos, vamos utilizar na hora de dimensionar os equipamentos.
Modelos de distribuição de tamanhos
Os modelos de distribuição de tamanhos podem ser tanto para quanto para . Mas, vamos usar o pra termos apenas curvas crescentes, beleza? E se algum dia você precisar relacionar e , basta lembrar que:
Vamos ver, agora, alguns modelos pra descrever essas curvas de em função de :
Modelo de Gates, Gaudin e Schuhmann (GGS)
Esse é o mais simples que tem. A fórmula dele é:
Aí, se lembrarmos daquele gráfico genérico de uma curva :
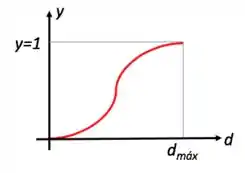
A gente vai ver que, para o modelo GGS:
Esse diâmetro representa um diâmetro de partícula tal que 100 % da massa da amostra correspondem a um diâmetro menor que esse. Por isso, que quando , fica igual a 1, estamos considerando todas as partículas da amostra menor que o diâmetro máximo!
Mais uma coisa MUITOOOO importante: e se eu te der uma tabela com valores de e os relacionados, como você faria pra calcular os parâmetros do modelo, que no caso, são e ?
Você vai ter que linearizar o modelo e depois fazer uma regressão linear. Bora ver o passo a passo que você vai entender tudinho : )
Se aplicarmos dos dois lados:
Opa! Isso é uma reta. A equação de uma reta é:
Daí, comparando:
Daí, vamos na calculadora e lançamos os valores de versus e pedimos pra ela fazer uma regressão linear. Aí ela nos diz os valores de e e usamos eles pra calcular e .
A calculadora também fornece os valores de correlação de Pearson (r) e/ou o , que é o quadrado do r; quanto mais próximo de , o módulo de r e forem, mais próximo do linear essa reta está, o que significa que melhor os seus pontos são representados pelo modelo proposto.
Atenção: se tiver ponto com ou na tabela que te derem, você despreza!!! Corta eles da sua tabela porque eles estão associados com muita incerteza.
Modelo de Rosin, Rammler e Bennett (RRB)
Para o RRB, a fórmula de y em função de d é dada por :
Em que é o correspondente a :
Da mesma forma que no GGS, precisamos linearizar o modelo pra achar os parâmetros do modelo, que são e . A forma linearizada fica:
Eu não vou gastar muito tempo aqui na teoria mostrando passo a passo dessas linearizações, ok? Vou colocar um exercício resolvido depois com o passo a passo de todas as elas.
Modelo Sigmóide
Para o Sigmóide, a fórmula é:
Em que é o diâmetro correspondente a . Ou seja, é a mediana da distribuição.
E a forma linearizada fica:
Modelo Log-Normal
Algumas vezes, a distribuição de frequência () fica parecendo uma gaussiana. Inspirado nisso que esse modelo surgiu.
Muita calma nessa hora. Vamos ver o que esses termos que aparecem aí significam:
“Tá. E daí? Eu quero é fórmula!” Ok. Vamos por partes
A função erro (erf) é tabelada. Então não se preocupa muito com ela não. Quanto aos outros dois:
E ,agora, presta atenção: o modelo log-Normal NÃO é linearizável. Daí, pra calcular os parâmetros dele vamos ter que usar algum método gráfico, colocar os pontos no papel num gráfico e liga-los e aí estimar os parâmetros. Relaxa que nos exercícios vemos isso melhor, ok?
Modelo Weibull
Até agora, todos esses modelos que mostrei pra você têm o zero como diâmetro mínimo, daí as curvas deles passarem pela origem. Mas e se ? Chora? Não, né. Nesse caso, vamos usar o Weibull, que considera que a distribuição NÃO começa na origem, ou seja, . A fórmula dele é:
Em que
Caso você esteja pensando “nossa, esse modelo é parecido com o RRB, né?”, é mesmo haha Ele é, basicamente, a curva do RRB mas deslocada no eixo de .
Agora preciso de falar uma coisa antes de mostrar a forma linearizada do modelo: uma reta tem parâmetros; pra você linearizar alguma coisa, essa coisa tem que ter exatamente parâmetros a serem determinados, assim como a reta. Daí, a principio, você não teria como linearizar o Weibull, MASSSS, se conhecermos o valor de , daí sobram 2 parâmetros e dá pra linearizar. Aí fica tipo a do RRB, mas no lugar de , vai ter um . Olha só:
Para saber o , temos casos: ou ele é dado (forma mais simples haha) ou então estimamos graficamente.
“Qual o melhor modelo?”
Fechamos os modelos já. Agora que comentar rapidinho com você sobre essa pergunta: “Qual o melhor modelo?”.
A resposta é fácil: depende. Cada amostra é uma amostra; pode ser que uma seja melhor representada por um modelo e outra por outro. Pra determinar isso, você compara aqueles coeficientes que falei (r e/ou ). Quanto mais próximo, em módulo, de “1” o coeficiente for, melhor aquele modelo representa tal amostra.
Resumão do Procedimento
Se o problema pede para você achar o melhor modelo ou verificar se um determinado modelo descreve bem a amostra:
1. Completar a tabela de dados de peneiração com os valores de , em base unitária.
2. Caso tenha informação sobre o mesh das peneiras, buscar na tabela o diâmetro equivalente. Se não tiver, o problema já vai fornecer o diâmetro para facilitar!
3. Selecionar os modelos e calcular os eixos e para cada modelo.
4. Jogar os dados dos eixos e na calculadora e ela vai calcular o coeficiente angular , coeficiente linear e o .
5. Veja se o está próximo de um e se for o caso compare diversos modelos.
6. Use os coeficientes angulares e lineares para estimar os parâmetros dos modelos!
A tabela abaixo resume os coeficientes e eixos de cada modelo:
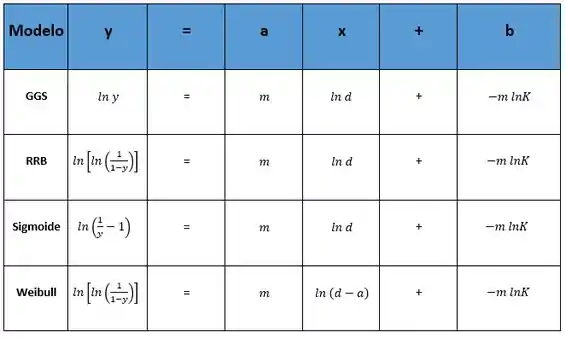
Se for um problema que já diz os parâmetros dos modelos e te pede alguma informação:
1.Identificar qual é o modelo.
2.Substituir os parâmetros na equação.
3.E se pedir o , vai te dar o diâmetro, e vice-versa!
Última coisa que preciso comentar, lembra que o diâmetro da peneira (e diâmetro da partícula ( não são a mesma coisa. Então, fica muito atento que dependendo do que a questão te pedir pode ser necessário converter esses diâmetros, beleza?
Modelo de Rosin, Rammler e Bennett (RRB)
Modelo Sigmóide
Modelo Log-Normal
Modelo Weibull
“Qual o melhor modelo?”
Resumão do Procedimento
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Lista 1 Prof. Medronho, Questão 9 – Adaptado
Calcule os parâmetros do modelo GGS para a seguinte amostra:
Passo 1
Temos pares e precisamos calcular os parâmetros do modelo GGS, que diz:
Sendo que os parâmetros dele são: e .
Para calcular esses parâmetros, vamos precisar linearizar o modelo e fazer regressão linear. A forma linearizada é:
Mas vamos nos organizar: primeiro de tudo, temos que trabalhar com em base unitária em todas as contas. Daí:
Passo 2
Comparando a forma linearizada ( ) com a equação de uma reta ():
Daí, vamos ter que montar uma tabelinha com e :
Vamos fazer uma regressão linear com os pontos ( , ):
Aí, temos que:
De cara, já obtivemos . Agora é só calcular o :
Substituindo o :
Cortando os “menos” e passando o para a direita dividindo:
E, como os diâmetros estão em :
Resposta
Exercício Resolvido #2
UFRJ - Lista 1 Prof. Medronho, Questão 9
A peneiração de uma amostra de areia gerou a seguinte distribuição de tamanhos:
Pede-se:
- Dentre os modelos GGS, sigmóide e RRB, indicar qual melhor descreve a referida análise.
Passo 1
Nessa questão, ele deu pares () e pede qual o melhor modelo dentre o GGS, sigmóide e RRB. Vamos ter que avaliar o coeficiente de correlação depois de linearizar e jogar na calculadora: quanto mais próximo de o coeficiente de correlação for, significa que melhor o tal modelo representa a amostra.
Vou trabalhar com o (se você preferir, pode usar o r; a ideia é a mesma).
Primeiro de tudo, temos que usar o em base unitária em todas as contas, então, vou adicionar uma linha nessa tabela aí logo:
E, como eu te disse lá na teoria, vamos desprezar, para linearizações, pontos com e pontos com . Daí, vou cortar logo esse último ponto aí:
Bora ver agora um por um:
Passo 2
Primeiro, bora ver o GGS. A fórmula pra no GGS é:
Linearizando, fica:
Daí, vamos ter que montar uma tabelinha com e :
Como vimos na teoria, comparando essa nossa equação linearizada com a equação de uma reta, :
Daí, vamos fazer uma regressão linear com os pontos ( , ):
Para avaliar qual o melhor modelo pra representar uma amostra, só precisamos dessa informação aí de . Então guarda aí:
Passo 3
Vamos ver, agora, o Sigmóide. A fórmula dele pra é:
Linearizando:
Comparando com a equação de uma reta:
Montando nossa tabelinha com e :
Fazendo a regressão linear:
Guarda aí, também:
Passo 4
Falta só o RRB agora. Bora lá! A fórmula de para o RRB é:
Linearizando:
Comparando com a equação de uma reta:
Fazendo a tabelinha com e :
Fazendo a regressão linear:
Guarda aí:
Passo 5
O mais trabalhoso já foi. Agora é só comparar os dos 3 modelos.
Como é o maior dentre os , isto é, o mais próximo de , o RRB é o melhor modelo pra representar ESSA AMOSTRA.
Resposta
RRB, pois o da sua linearização é o mais próximo de 1, ou seja, o maior dentre os modelos analisados.
Exercício Resolvido #3
Elaboração própria
Mostre o passo a passo da linearização dos seguintes modelos:
- RRB
- Sigmóide
- Weibull (assuma que o parâmetro é conhecido)
Passo 1
Eu não esqueci que essa matéria é operações unitárias não, tá? Mas coloquei essa questão de mostrar o passo a passo da linearização por que, provavelmente, na prova você não vai ter os modelos linearizados e sim as equações pra no formulário. Daí, pra achar os parâmetros dos modelos você vai ter que desenvolver a linearização ali na hora (a menos que tenha decorado as formas linearizadas né haha mas eu prefiro fazer na hora).
Bora reunir aqui as equações desses três modelos e depois partimos pra linearizar um por um.
Antes de começarmos, deixa eu te falar uma coisa: quando formos fazendo operações pra deixar linear, temos que fazer um caminho “reversível”. O que eu quero dizer com isso é que você tem que transformar uma coisa em outra que seja possível de ser “retransformada”. Tipo assim, se tem lá um , você pode aplicar dos dois lados:
Isso porque se você aplica exponencial () dos dois lados, volta ao inicial:
Agora, se o aparecer , você NÃOOO pode aplicar , porque e aí esse termo desaparece.
Bora ver essas linearizações que você vai entender melhor tudo isso, ok?
Passo 2
- RRB
- Sigmóide
- Weibull (assuma que o parâmetro é conhecido)
A equação de em função de para o modelo RRB é:
Não podemos aplicar direto porque iria aparecer um . Daí bora jogar a exponencial para a esquerda e o para a direita:
Vou reescrever essa exponencial com aquela notação com só pra facilitar a visualização; mas é a mesma coisa; não vou mudar nada:
E isso é a mesma coisa que:
Rearranjando:
Agora sim podemos aplicar dos dois lados:
Mas ainda tem um expoente ali...ainda não tá linear. Mas se aplicar outra vez dos dois lados fica. Daí:
Pronto. Um já foi.
Passo 3
A equação de em função de para o modelo Sigmóide é:
De novo, não podemos aplicar aqui porque iria aparecer um . Bora fazer outra coisa então. Vamos inverter os dois lados:
Passando esse pra esquerda:
E agora aplicamos dos dois lados:
Passo 4
Lembrando que ele fala que o parâmetro é conhecido porque uma reta tem 2 parâmetros ( e ) e o modelo Weibull tem 3, e , daí, não daria pra linearizar. Mas se o é conhecido, sobram 2 parâmetros a se conhecer e aí conseguimos linearizar.
O Weibull é muito parecido com o RRB e a linearização segue a mesma linha, mas substituindo onde tem por .
A equação de em função de para o modelo Weibull é:
Não podemos aplicar direto porque iria aparecer um . Daí bora jogar a exponencial para a esquerda e o para a direita:
Vou reescrever essa exponencial com aquela notação com só pra facilitar a visualização; mas é a mesma coisa; não vou mudar nada:
E isso é a mesma coisa que:
Rearranjando:
Agora sim podemos aplicar dos dois lados:
Mas ainda tem um expoente ali...ainda não tá linear. Mas se aplicar outra vez dos dois lados fica. Daí:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
UFRJ - Lista 1 Prof. Medronho, Questão 11 - Adaptado
Estimar os parâmetros do modelo de Weibull para a seguinte amostra:
Passo 1
Nessa questão, temos uma tabela com pares (), com o diâmetro em , e é pedido para estimar os parâmetros do modelo Weibull para essa amostra. Bora lembrar da equação de para esse modelo:
Os parâmetros dele são: e . Ou seja, 3 parâmetros para determinar.
Como vimos na teoria, uma reta tem 2 parâmetros então não dá pra linearizar o Weibull assim, com esses 3 parâmetros desconhecido. Mas se tivermos como determinar algum deles, conseguimos linearizar, já que só vão sobrar 2 parâmetros.
Passo 2
A primeira coisa pra fazer é determinar o , que é o parâmetro que temos como estimar graficamente. Dessa forma, vão sobrar 2 parâmetros a determinar e aí conseguimos linearizar e fazer regressão linear para calcular e . Bora lançar esses pares () num gráfico:
Numa prova, você faria lançaria esses pontos num papel milimetrado.
Depois, o que temos que fazer é traçar a mão a curva , passando por esses pontos. Daí, vemos a interseção da curva com o eixo , que é o eixo do diâmetro, e esse será o , isto é, o parâmetro . Vou fazer isso agora, dando um zoom nos pontos mais próximos desse pra facilitar da gente enxergar o :
Daí:
Passo 3
Agora que temos o , só restam 2 parâmetros a determinar e aí conseguimos linearizar e fazer regressão linear. Como vimos na teoria, a forma linearizada da equação de Weibull, conhecido o , é:
Comparando com a equação de uma reta, :
Daí, precisamos de uma tabela com os pares (), isto é, pares ( ), lembrando que, na hora de linearizar, desprezamos pontos com e/ou .
Fazendo a regressão linear:
Daí:
E
Substituindo o valor de nessa ultima equação:
Cortando os menos e isolando :
E como os diâmetros estão em :
Resposta
Exercício Resolvido #5
Elaboração própria
Calcule os parâmetros do modelo log-normal para a seguinte amostra:
Passo 1
Temos uma tabela com pares (), com diâmetros em e temos que calcular os parâmetros do modelo log-normal. A grande questão desse exercício é que o modelo log-normal NÃO é linearizável. Portanto, vamos ter que resolver graficamente.
Vamos começar plotando, num gráfico, . Vou fazer no excel, mas se fosse em uma prova, você provavelmente teria papel milimetrado.
Vamos precisar, também, traçar um esboço do formato da curva , passando por esses pontos. No papel milimetrado, você faria à mão livre mesmo. Como estou no excel, vou pedir pra ele um gráfico com linhas suaves:
Passo 2
A expressão para , isto é, em função do diâmetro, segundo o modelo log-normal, é:
Seus parâmetros são e . Lembrando, da teoria, como calcular cada um deles:
Então, temos que ir no gráfico e pegar pontos. Bora começar com o . Daí, precisamos achar o diâmetro que faz .
Eu coloquei “aproximadamente” porque estamos trabalhando com método gráfico, daí, estamos obtendo estimativas né.
Agora, falta calcular o . Para isso, precisamos ou do ou do . Vou pegar o .
E bota aproximado nisso! Mas estamos no método gráfico então há limitações né.
Calculando :
Resposta
Exercício Resolvido #6
UFRJ - Lista 1 Prof. Medronho, Questão 12
A análise granulométrica de uma amostra de minério de barita originário de Itaguaí-RJ é fornecida abaixo:
b) Elaborar o ajuste dos modelos de distribuição granulométrica GGS, Sigmóide e RRB e selecionar o mais adequado.
Passo 1
Temos os dados obtidos na peneiração de uma amostra e queremos calcular a curva por 3 modelos diferentes: GGS, Sigmóide e RRB.
Precisamos passar as designações Mesh Tyler das peneiras para diâmetro da abertura da peneira já que calcular os parâmetros de cada modelo, vamos precisar de pares ().
Também vamos precisar das frequências , já que calculamos os da seguinte forma:
Daí, bora calcular os
Vamos precisar do :
Agora podemos calcular o associado a cada faixa. Para a primeira, por exemplo, fica:
Aí, convertendo os para diâmetro e adicionando os (com base no ):
Repara que já coloquei e em base unitária para não nos confundirmos : )
Para calcular as curvas de distribuição de tamanho , só o que nos interessa são os pares (). Vou destaca-los na tabela:
Bora calcular agora modelo por modelo as curvas .
Passo 2
GGS: A curva desse modelo tem essa cara:
Como já vimos lá no tópico de distribuição de tamanhos, pra calcular os parâmetros, precisamos linearizar essa equação e fazer regressão linear. A forma linearizada fica:
Fazendo uma tabela com os valores de e e fazendo regressão linear:
Comparando com a equação da reta, :
Calculando o valor de :
Daí:
E lembra aí do que veio da regressão linear.
Passo 3
Sigmóide: A curva desse modelo tem essa cara:
E a forma linearizada é:
Daí:
Comparando com a equação da reta, :
Daí:
E lembra aí do que veio da regressão linear.
Passo 4
RRB: A curva desse modelo tem essa cara:
E a forma linearizada fica:
Comparando com a equação da reta, :
Aí a curva fica:
Comparando o entre os três modelos, o maior de todos é o GGS. Então, esse é o melhor modelo para representar essa amostra.
Resposta
O modelo mais adequado para essa amostra é o GGS, já que está associado com o maior valor de .