Introdução à Distribuição de Tamanhos
Produzido por Marcelo AlvesTeoria
Introdução
Nesse tópico a gente vai falar de distribuição de tamanhos. Primeiro de tudo, precisamos entender o que é isso, né?
Vamos começar relembrando um pouquinho de peneiração? Quando passamos uma amostra com partículas de diferentes diâmetros por um conjunto de peneiras, conseguimos montar uma tabela que resume a massa que ficou entre cada par de peneiras, tipo essa tabela abaixo:
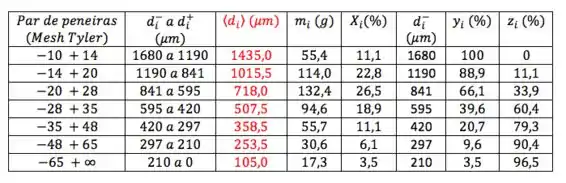
Se você tá perdido sobre como essa tabela foi obtida, fica tranquilo que em peneiração tem o passo-a-passo completinho!

Mas, generalizando, podemos interpretar essa tabela como a massa de amostra, , que ficou retida entre cada par de peneiras. E cada par, por sua vez, possui um diâmetro equivalente a cada peneira, que é tabelado.
Além disso, nessa tabela, vemos os cálculos dos valores , e . é a porcentagem de amostra retida entre dois diâmetros diferentes em relação a massa total de amostra.
Mas o que são e ? e são distribuições cumulativas. E, agora, vamos entender um pouquinho mais sobre essas curvas!
Curvas de distribuição cumulativa
As curvas de distribuição cumulativa são muito utilizadas quando queremos saber qual a porcentagem de partículas menores ou maiores que um certo diâmetro. Para ter essa informação, você teria que ver quantos por cento da área total debaixo da curva estão abaixo ou acima desse tal diâmetro.
Há dois tipos de distribuições cumulativas.
Bora ver melhor a que é mais utilizada:
Distribuição cumulativa menor que dado ()
O gráfico dela é uma curva em S que está sempre subindo. Colocando os dados da tabela em um gráfico, é esse o tipo de curva que obtemos:
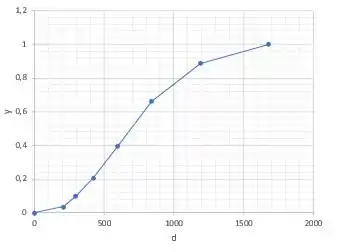
“Mas como eu uso isso?” A melhor forma de explicar isso é com um exemplo. Saca só:
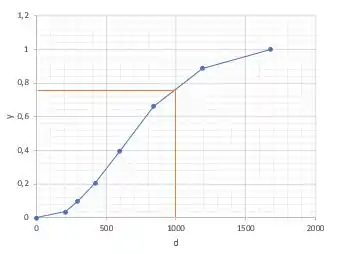
Eu leio esse ponto marcado como: “ 0,76 ou das partículas possuem diâmetro menor que ” . Então, cada par () nos dá a fração de partículas com diâmetro menor que naquela amostra.
Mas concorda comigo que num conjunto de partículas vai ter um diâmetro que vai ser o maior de todos, ? Daí, vamos dizer que abaixo desse diâmetro estão das partículas. Como vamos trabalhar com em base unitária, associamos com .
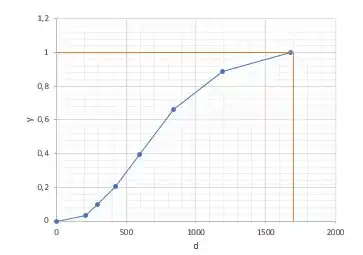
Distribuição cumulativa maior que dado ()
Enquanto a distribuição cumulativa menor que dado d () nos diz a parcela das partículas com diâmetro abaixo de um diâmetro , a distribuição cumulativa maior que dado () nos diz a parcela das partículas que tem diâmetro maior que dado d. Chegamos em por:
Aí a cara dela é tipo assim:
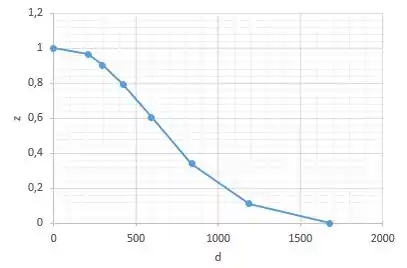
E na hora de ler os pontos, olha esse exemplo:
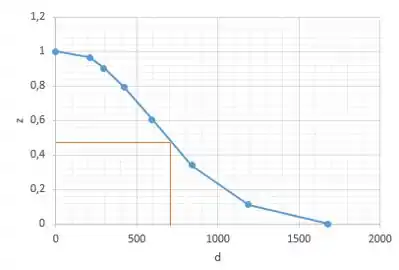
A gente vai ler: “ , ou seja, 48% das partículas tem diâmetro maior que .”
Talvez você esteja se perguntando qual diâmetro da tabela que entra nesses gráficos... Na tabela, temos ,e , mas, geralmente, o não é utilizado para montar esses gráficos! Então, você pode utilizar tanto o desde que você utilize o mesmo para todos os pontos do gráfico, combinado? Nesse caso, optamos pelo , pois a sua interpretação é mais fácil!
Show? Por esse tópico é só. Até o próximo 😊
Curvas de distribuição cumulativa
Distribuição cumulativa menor que dado d ( y )
Distribuição cumulativa maior que dado d ( z )
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Um engenheiro obteve uma amostra de areia e estava interessado em saber quantos por cento da amostra possuía um diâmetro superior a . Qual experimento esse engenheiro pode realizar para obter essa informação?

Passo 1
Vamos lá! Nessa questão, precisamos apenas indicar um experimento para determinar o quanto de massa de uma amostra possui um diâmetro superior a . Com essa massa, conseguimos determinar a porcentagem em relação ao total, certo?
Antes de mais nada, precisamos lembrar láááá de amostragem. Se a amostra for suficientemente pequena, vamos usar toda a amostra para a análise. Se não, devemos homogeneizar e usar uma tática de amostragem, como aquela em que colocamos a amostra em um “montinho”, dividimos o montinho em quatro partes e pegamos duas partes diagonalmente opostas (rejeitando o restante). Repetimos a operação até que a massa seja suficientemente pequena para a análise.
E aí, quando falamos de o quanto de massa possui um diâmetro MAIOR que um certo valor, podemos analisar as curvas do tipo z, certo?
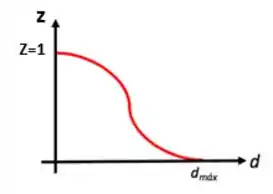
Passo 2
E como conseguimos essas curvas do tipo ? Para isso, basta a gente realizar o experimento de peneiração!
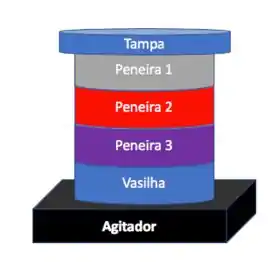
E aí, passando a amostra pelas peneiras, conseguimos obter a fração entre cada par de peneiras. Lembrando que:
Somando o até cada diâmetro, obtemos o , que é a distribuição cumulativa menor que dado diâmetro, certo?
E sabemos que . Então conseguimos achar a curva do tipo , ou seja, curva de distribuição cumulativa maior que dado diâmetro. Essa curva tem essa carinha aqui:
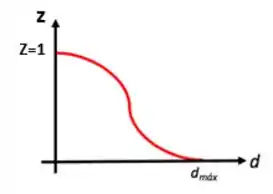
E aí seria só realizar a leitura do gráfico com as informações que o engenheiro quer!
Resposta
Peneiração
Exercício Resolvido #2
Elaboração própria
Uma amostra foi submetida ao peneiramento e como resultado foi dada a seguinte curva:
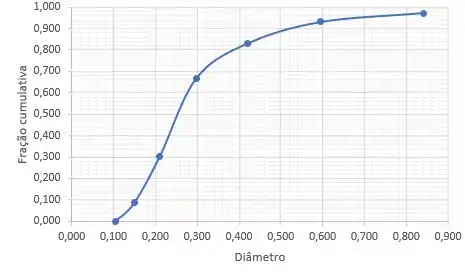
Sabendo que os diâmetros estão em milímetros, indique se essa curva representa a curva ou a curva e, além disso, indique a porcentagem da amostra menor e maior que .
Passo 1
Vamos começar revisando o formato das curvas.
A curva possui o seguinte formato:
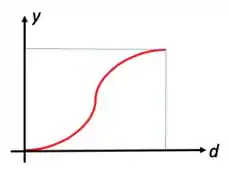
Enquanto a curva possui a seguinte forma:
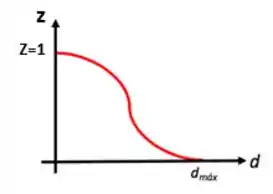
Portanto, a nossa curva é do tipo . Curvas do tipo representam a distribuição cumulativa menor que dado diâmetro, ou seja, quantos porcento da amostra são menores que o diâmetro que estamos lendo! Elas são crescentes, como a do enunciado!
Passo 2
Já vimos que a curva do enunciado é do tipo e indica a distribuição menor que dado diâmetro. Então, para encontrarmos a porcentagem menor que 0,7 mm, só precisamos olhar esse ponto na curva!
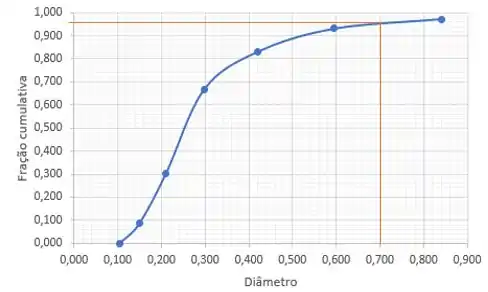
Logo, ou da amostra é menor que .
Passo 3
Quando falamos em encontrar a porcentagem maior que , estamos falando em calcular . Mas, sabemos que:
Então para calcular :
Assim da amostra é maior que .
Resposta
Curva do tipo .
da amostra é maior que .
96% da amostra é menor que .
Exercício Resolvido #3
Elaboração Própria
Uma amostra possui a seguinte curva do tipo com os diâmetros representados em milímetros.
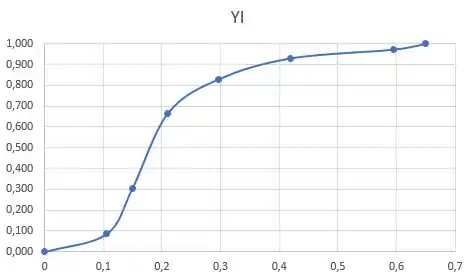
Qual é o diâmetro máximo ( dessa amostra, sabendo que o eixo x são os diâmetros ()?
Passo 1
O diâmetro máximo é o maior diâmetro daquela amostra, certo?
A curva do tipo representa as partículas menores que um dado diâmetro. Como queremos o maior diâmetro da amostra, basta olhar o local que o , pois indica que 100% da amostra é menor que ele! Logo, ele é o diâmetro máximo.
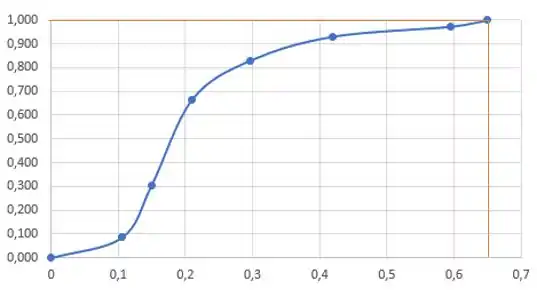
Portanto, .
Resposta
Exercício Resolvido #4
Elaboração Própria
Uma amostra possui a seguinte curva do tipo com os diâmetros representados em milímetros.
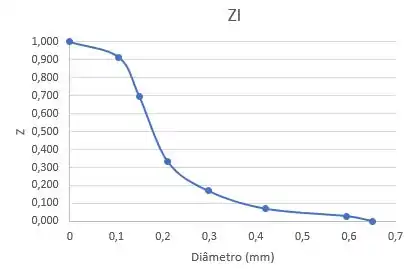
Qual é o diâmetro máximo ( dessa amostra, sabendo que o eixo x são os diâmetros ()?
Passo 1
O diâmetro máximo é o maior diâmetro daquela amostra, certo?
A curva do tipo representa as partículas maiores que um dado diâmetro. Como queremos o maior diâmetro da amostra, basta olhar o local que o , pois nada é maior que esse diâmetro, então esse é o maior da amostra!
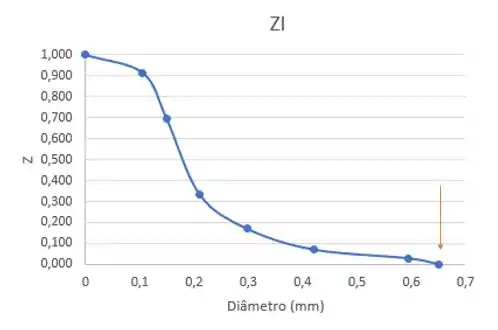
Portanto, .
Dica: Repara que comparando com a questão que analisamos a curva do tipo deu o mesmo diâmetro máximo! Isso indica que tanto faz usar a curva ou para uma mesma amostra 😊
Resposta
Exercício Resolvido #5
Elaboração Própria
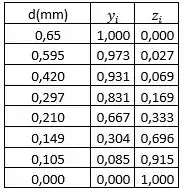
A partir do gráfico abaixo de uma distribuição de tamanho do tipo , determine os respectivos pontos para o tipo .
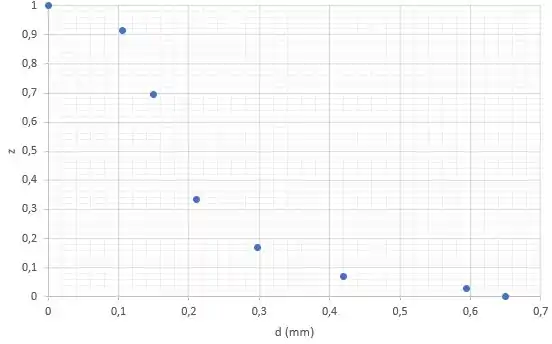
Passo 1
Sabemos que e estão relacionados da seguinte forma:
Assim, se soubermos os valores de para cada diâmetro, conseguimos calcular os respectivos . E os valores de estão no gráfico!
Passo 2
Extraindo os valores de diâmetro e de do gráfico, podemos construir a seguinte tabela:
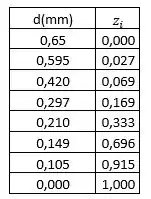
E, como , podemos calcular os valores de
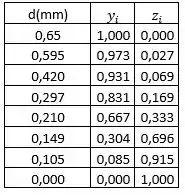
Fazendo para as primeiras linhas de exemplo:
E, depois, fizemos isso para todas as linhas. Prontinho!
Resposta
Exercício Resolvido #6
Elaboração Própria
Um analista recebeu a seguinte tabela sobre a peneiração de uma amostra:
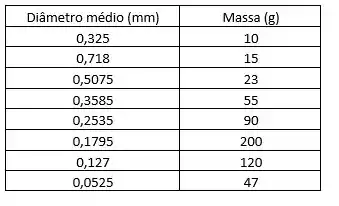
Obs: O diâmetro médio dado é o diâmetro médio entre as peneiras e .
Foi solicitado que apenas com esses dados fosse realizado uma curva de distribuição do tipo dessa amostra. Isso seria possível?
Passo 1
Vimos que para traçar as curvas de distribuição de tamanho precisamos saber ou . Assim, se só temos o diâmetro médio entre essas duas peneiras não podemos traçar a curva de distribuição. Então, o analista precisaria solicitar os dados das peneiras utilizadas ou refazer as análises!
Resposta
Não seria possível :/