Teoria
A Peneiração é uma Operação Unitária utilizada para separar sólidos de diferentes diâmetros
O que é Peneiração?
Na indústria, em muitos momentos é interessante separar as partículas de acordo com o seu diâmetro. Essa necessidade pode existir por diferentes motivos e um deles é deixar o produto dentro de uma especificação determinada para comercialização.
Para isso é utilizado a técnica de peneiração, que consiste na separação de sólidos de diferentes diâmetros a partir do uso de uma peneira.

Uma peneira, que nada mais é do que uma superfície com arames entrelaçados, que dão origem a passagens quadradas, como mostrado na figura acima.
🚨Uma observação importante é que vamos considerar as peneiras como equipamentos ideais de separação.
Na prática, isso significa que:
- Se
a partícula é retida; - Se $d_\text{partícula}
Associação de peneiras
Dificilmente você vai ver um experimento usando uma peneira só!
O que normalmente é feito é utilizar uma sequência de peneiras, com uma tampa em cima e uma vasilha de fundo embaixo, pra reter as partículas que passarem pela última peneira. Assim:
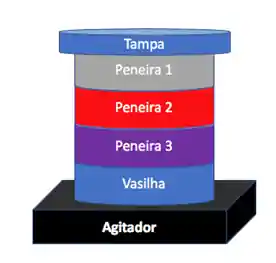
Na prática a peneiração com associação de peneiras acontece da seguinte forma:
Você coloca a amostra na peneira
Percebe que a abertura da peneira
Se a peneira
Abertura de peneiras
A abertura de peneiras é o espaço entre aqueles arames e indica o diâmetro da maior partícula que pode passar por ela (ou da menor que fica retida).

Algumas vezes, não sabemos diretamente a abertura da perneira. O que vai ser informado é o Mesh Tyler ou o número de peneira. Aí temos que usar uma tabela como essa aí de baixo, que relaciona esses caras com o diâmetro de abertura, que é o que realmente nos interessa.
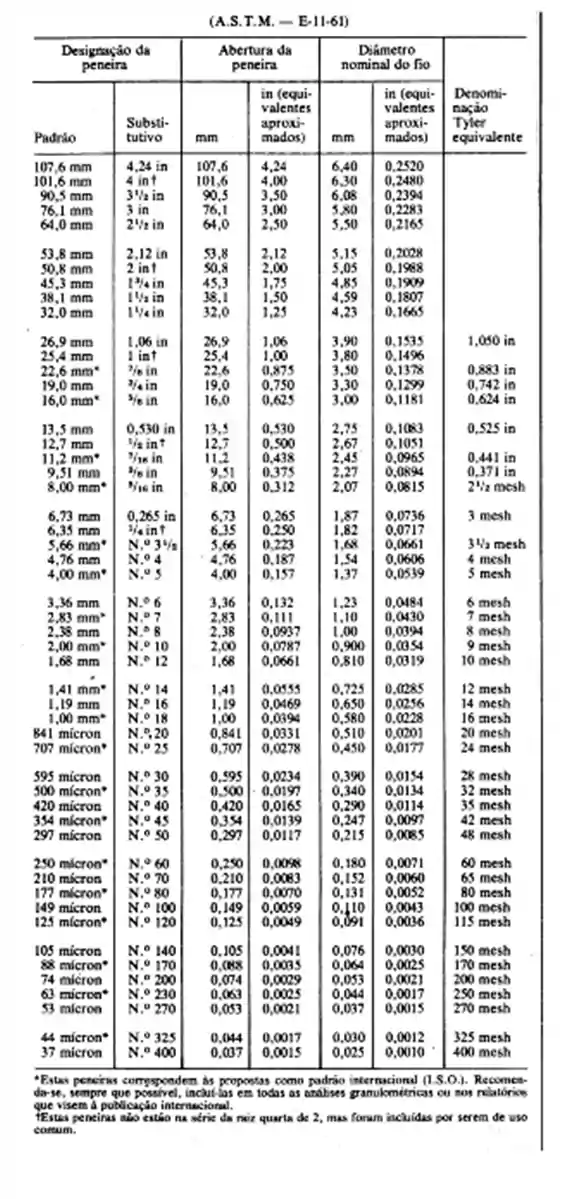
Então, uma peneira de
Outros Processos de Separação Física
Existem outros processos de separação física que são um pouco parecidos com a peneiração. Então vamos conhecer um pouquinho sobre eles pra não ter risco de confundir no futuro!
Levigação
Levigação também é um método de separação de sólidos e também é feita com o auxílio de uma espécie de peneira.
Diferente da peneiração, ela é baseada da diferença de densidade das partículas. Além disso, para realizar a levigação, pode-se utilizar uma corrente de água.
Um exemplo muito comum da aplicação de Levigação é na separação de ouro no garimpo. Nesse caso a parte menos densa (terra) é carregada junto com a água e as partículas mais pesadas (ouro) fica retida na peneira.
Ventilação
A ventilação também se baseia na diferença de densidade das substâncias. Como o próprio nome sugere, uma mistura é submetida a uma corrente de ar. Dessa forma, as substâncias menos densas são arrastadas pelo vento e as mais densas permanecem retidas.
Agora, bora praticar com exercícios?!