Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Determine o poder calorífico superior da mistura combustível em por .
Passo 1
Faaala, pessoal! Diz aí: vocês sabem o que é determinar o poder calorífico superior?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico superior é feito considerando que a combustão gera apenas líquido. A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Nós podemos calcular direto, porque a composição do combustível foi dada em base mássica (porcentagem de massa)!

Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares, precisamos escrever a equação de combustão para uma vazão mássica total de do gás combustível composto de , , , e .
Consideramos que de gás está reagindo, porque a composição da mistura combustível é dada em porcentagens de massa! Veremos como essa escolha vai facilitar nossa vida!
onde , , , , , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são as vazões molares das substâncias. Por exemplo, é a vazão molar de e é a vazão molar de . Pra achar a vazão molar de , achamos a vazão mássica de , multiplicando a vazão total de de combustível pelos de do combustível!
Dividindo esse valor pela massa molar de , que vale , encontramos a vazão molar de !
Usamos o mesmo método pra determinar a vazão de . Primeiro, achamos a vazão mássica , multiplicando a vazão total de de combustível pela porcentagem de presente no combustível.
Depois, dividimos essa vazão mássica pela massa molar pra achar o valor da vazão molar de . vale .
Vamos usar o mesmo passo a passo pra achar as vazões molares , e de , e . Novamente multiplicamos as porcentagens pela vazão total de pra achar as vazões mássicas. Por fim, dividimos as vazões mássicas pelas massas molares pra achar as vazões molares! Começamos pelo que representa do carvão.
Dividindo essa vazão pela massa molar , achamos o coeficiente .
O representa do combustível. Logo:
Dividindo essa vazão pela massa molar , achamos o coeficiente .
Por fim, achamos o coeficiente que é a vazão molar de . representa do combustível.
Dividindo essa vazão pela massa molar , achamos o coeficiente .
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Faremos o balanço no próximo passo!
Passo 3
Encontramos o coeficiente , através do balanço de carbono . Os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Encontramos o coeficiente de por meio do balanço de . Os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente é determinado pelo balanço de . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação de , , , e valem zero, porque eles são substâncias quimicamente mais estáveis.
A entalpia de formação do , de e pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação da água líquida, porque o enunciado quer o poder calorífico superior da combustão !
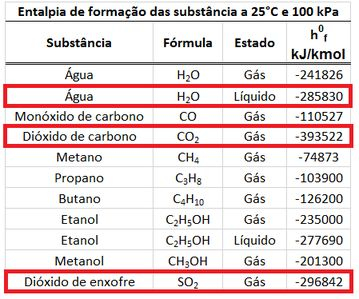
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Shoe de bola, pessoal! Calculamos o que o enunciado nos pediu!