Determine a entalpia de formação do fenol , sabendo que o poder calorífico inferior do fenol vale .
Passo 1
Fala, pessoal! Perceberam que esse exercício é invertido? Geralmente, conhecemos as entalpias de formação e a questão pede o poder calorífico do combustível. No entanto, esse exercício faz o contrário! Ele nos dá o poder calorífico da combustão do e pede a entalpia de formação do . Para calcular , usaremos a primeira lei abaixo.
é a taxa de calor trocada. é a taxa de trabalho realizada. é a vazão molar dos reagentes e é a vazão molar dos produtos.
Como o poder calorífico inferior é o calor liberado pela queima de combustível, a taxa de calor trocada é igual a com um sinal de menos na frente!
Além disso, o exercício não fala nada sobre realização de trabalho durante a combustão. Por isso, a taxa de trabalho vale zero!
Já conhecemos dois valores da primeira lei. No entanto, precisamos aprender a calcular os somatórios. Pra achar a entalpia de formação do que queremos!
Passo 2
Para calcular os somatórios, precisamos saber o valor das vazões molares dos reagentes e dos produtos . Descobrimos isso, escrevendo a equação de combustão completa de reagindo com puro.
onde , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de e é a vazão molar de .
Consideramos que de está reagindo, porque é o calor liberado por unidade de combustível queimado! Logo, a vazão molar de vale:
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão. Ou seja, encontramos , e igualando os elementos dos reagentes aos elementos dos produtos! Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Com esses valores, somos capazes de achar os somatórios e e de calcular do fenol.
Passo 3
O somatório dos reagentes é a soma das entalpias dos reagentes e .
A entalpia de formação do vale zero, porque é uma substância quimicamente mais estável. Além disso, os dos reagentes valem zero, porque eles estão a . Substituindo
essas informações no cálculo do somatório dos reagentes:
No próximo passo descobrimos quanto vale o somatório dos produtos!
Passo 4
O somatório dos reagentes é a soma das entalpias dos produtos e .
A entalpia de formação do e de pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
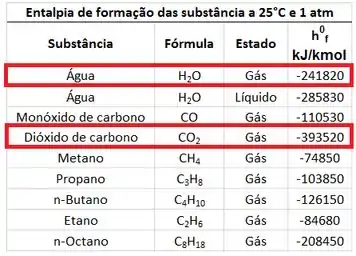
Além disso, os dos produtos valem zero, porque eles estão a . Substituindo
essas informações no cálculo do somatório dos produtos:
Agora podemos substituir os valores na primeira lei e achar a entalpia de formação!
Passo 5
Sem enrolação, vamos substituir direto os resultados das nossas contas na equação da primeira lei!
Uhuuuuul! Arrasamos! Encontramos o resultado que o enunciado pediu!