O gás combustível, produzido num fermentador de biomassa, apresenta a seguinte composição (em base molar): de metano, de dióxido de carbono e de hidrogênio. Determine o poder calorífico inferior deste gás combustível por unidade de volume.
Passo 1
Oi, galerinha! Vocês sabem o que é determinar o poder calorífico inferior?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico inferior é feito considerando que a combustão gera apenas vapor de . A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Pra calcular o poder calorífico do combustível por unidade de volume (em por ), usamos a equação de gás perfeito abaixo.
onde é a pressão do gás combustível que vale (pressão atmosférica aproximada) pro cálculo de . é a constante universal do gás ideal que vale . é a temperatura de do gás em kelvin . Multiplicando por , achamos o poder calorífico do gás por unidade de volume.
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares, precisamos escrever a equação de combustão para uma vazão molar total de do gás combustível composto de , e .
Consideramos que de gás está reagindo, porque é o calor liberado por unidade de combustível queimado!
onde , , , , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de , é a vazão molar de , é a vazão molar de , é a vazão molar de e é a vazão molar de . Pra achar a vazão molar de precisamos multiplicar a vazão total de pelos de do combustível!
Usamos o mesmo método pra determinar a vazão de dos reagentes. Multiplicamos a vazão total de de gás combustível pela porcentagem de presente no gás.
Por fim, achamos a vazão de do mesmo jeito! Multiplicamos a vazão total de gás combustível pela porcentagem de presente no gás.
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Faremos o balanço no próximo passo!
Passo 3
Encontramos , através do balanço de carbono . Os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação de e vale zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do , de e do pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
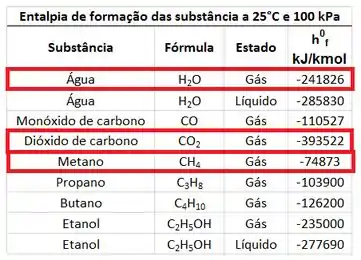
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Agora, vamos descobrir quanto nave do gás combustível pra poder converter o poder calorífico de pra .
Lembrando, é a pressão do gás combustível que vale (pressão atmosférica aproximada). é a constante universal do gás ideal que vale . é a temperatura de do gás em kelvin . Substituindo esses dados:
Multiplciando por :
Uhuuuuuul! Mandamos muito!