Intervalo de Confiança para Variância Populacional
Teoria
IC para Variância Populacional
Tá, já vimos intervalo de confiança para média populacional, proporção populacional...
Aí você ficou empolgado, achando que tinha acabado... sqn! Haha
Faltou adivinhem ? Intervalo de confiança para a variância populacional .
Vai parecer meio complicado, mas não se assustem, vai dar tudo certo!
Bom...
Algo lógico: se a gente tá procurando um intervalo de confiança para a variância é porque a gente não conhece o valor exato dela , concorda? Beleza.
Então vamos tentar achar uma relação entre e sua estimativa amostral .
A gente sabe que:
Continuando... divido tudo por :
Até aí foi?
Agora vem o pulo do gato, uma novidade que você vai adorar, ou não.
Vamos dizer que:
Substituindo no início, descobrimos que:
Ou..
WTF?
Vamos falar agora melhor sobre essa novidade aí.
Qui-Quadrado
A novidade que apareceu ali é uma nova distribuição (como a Normal e a T de Student) que vai ajudar a gente a fazer nosso intervalo de confiança.
Mais uma distribuição, mais uma tabelinha... Distribuição . “Qui” é o nome dessa letra aí , só por curiosidade mesmo.
Calma jovem, as coisas vão ficar mais humanas, sem desesperos. No final, é tudo continha.
Vou te ensinar primeiro como usar a tabela .
Os parâmetros que a gente vai precisar são:
E valores de pra acharmos na tabela.
Mesma coisa que .
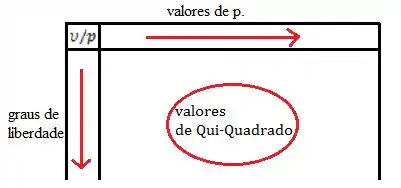
A diferença é que se antes era comum procurarmos por valores de , agora além de um , iremos procurar também por .
Você vai entender melhor já já!
Podemos representar assim também oh:
Testando...
- Achar o valor de
Cruzando a linha 10 com a coluna 0,995.
Foi ?
O Intervalo de Confiança
Tá, agora vamos transformar tudo isso que eu disse em algo mais prático, que é o que interessa de verdade.
Para o caso do para a média a gente tinha...
Lembra?
Nada mudou..
Atualizando isso para o caso da variância, usando nosso novo amigo .
Agora vem uma última novidade, esses valores inferior e superior são definidos como:
Lembra que eu disse que a gente ia precisar do e do ?
Anota na testa! Hehe..
Voltando....
A gente sabe que:
Substituindo:
Mas eu quero um intervalo para a . Posso inverter tudo então, você deixa? Beleza...
Estamos quase lá... multiplico geral por :
Fim!
Nosso intervalo de confiança para a variância com de confiança será:
E se você quiser fazer algo com relação ao desvio padrão , de boas, só tirar raiz quadrada de geral.
Vlw, flws..
Vamos de exercícios agora.
Qui-Quadrado
O Intervalo de Confiança
Exercícios Resolvidos
Exercício Resolvido #1
PUC – 2013.2 – P3 -Intervalo de Confiança – Qui Quadrado
Uma fábrica de alimentos comercializa sacos de feijão para pequenos supermercados. Toma-se uma amostra com sacos de feijão de uma determinada população, com média igual a e variância igual .
- O intervalo de confiança de e para a variância da normal desta população.
Passo 1
A gente tem os dados da amostra:
E vamos montar dois intervalos de confiança para a variância populacional, .
Esses dois intervalos são feitos da mesma maneira, tem a mesma cara... que é:
Aí esses valores de baixo são os que a gente pega na tabela .
E são eles que vão mudar em cada intervalo, porque dependem do .
Passo 2
Quem é ? Quando o intervalo é de ...
Aí a gente precisa do e do .
O número de graus de liberdade é
Podemos procurar na tabela já... cruzando a linha do com as duas colunas certas.. a gente tem:
Passo 3
Agora é só jogar na fórmula do intervalo, já temos tudo!
Passo 4
Se o intervalo é de ...
Aí a gente precisa do e do .
O número de graus de liberdade é
Podemos procurar na tabela já... cruzando a linha do com as duas colunas certas.. a gente tem:
Passo 5
Só jogar na fórmula de novo
Resposta
Exercício Resolvido #2
PUC – 2011.1 – P3 - Intervalo de Confiança – Qui Quadrado
Seja uma variável aleatória contínua que segue uma Normal com média e variância , ambas desconhecidas.
Seja , uma amostra aleatória de tamanho desta população:
Pede-se:
b) O intervalo de confiança ao nível de confiança de , para .
Passo 1
(b)
Agora partiu fazer um intervalo de confiança para a variância.
A gente sabe que o intervalo de confiança nesses casos tem a seguinte cara:
E que:
É só a gente calcular cada parte.
Sabendo que e .
Passo 2
Passo 3
Agora só completar o .
Resposta
Exercício Resolvido #3
PUC – 2012.2 – P3 -Intervalo de Confiança – Qui Quadrado
Seja uma variável aleatória contínua que segue uma Normal com média e variância , ambas desconhecidas. Toma-se um amostra de tamanho igual a de uma determinada população, com média igual a e variância igual a .
Pede-se:
- O intervalo de confiança de para a variância da normal desta população.
Passo 1
(a)
A gente não conhece os parâmetros da normal da população, e vamos estimar eles usando os dados que a gente tem da amostra..
Passo 2
Primeiro vamos fazer um intervalo para a variância .
Você lembra a cara desse intervalo? Vou recordar pra você aqui..
Aí esses valores de baixo são os que a gente pega na tabela .
Passo 3
Vamos achar os valores da tabela...
Quem é ? Se o intervalo é de ...
Aí a gente precisa do e do .
O número de graus de liberdade é
Podemos procurar na tabela já... cruzando a linha do com as duas colunas certas.. a gente tem:
Passo 4
Agora é só jogar na fórmula do intervalo, já temos tudo!
Resposta
Exercício Resolvido #4
Lista Regina – CEFET Intervalo de Confiança – Qui Quadrado
Um cano deve ser colocado em um fresta já existente. Se o desvio-padrão do diâmetro do cano exceder 0,01mm, haverá uma probabilidade inaceitavelmente alta de que o cano não se ajuste. Uma amostra aleatória de peças é selecionada e o diâmetro de cada cano é medido. O desvio-padrão do cano é . Construa um intervalo de confiança de 99% para a variância verdadeira da peça. O cano poderá ser colocado nesta fresta?
Passo 1
Vamos aos dados do problema primeiro:
Pedem pra gente fazer um intervalo de confiança para a variância verdadeira da peça com 99% de confiança.
Intervalo de confiança pra variância você já está ligado que vamos usar
Passo 2
Pelo que aprendemos, a gente sabe que o terá a cara:
Vamos calcular o que falta então:
Como a confiança é de 99%.
e...
Já que são 14 graus de liberdade, concorda?
Passo 3
Agora sim...
Podemos calcular o .
Para achar o para o caso do desvio padrão, basta tirar a raiz, aí ficaria:
Passo 4
O exercício diz que o diâmetro exceder 0,01 existe grande chance do cano não se ajustar a fresta.
Como no nosso intervalo abrange o valor de 0,01 de desvio padrão, significa que há chance dele exceder 0,01 ... isso significa que o cano não deveria ser colocado na fresta.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Prof. Luiz A. Peternelli – DPI, UFV.
Tintas para marcação em asfalto de rodovias são oferecidas em duas cores, branca e amarela. O tempo de secagem dessas tintas é de muito interesse, e especificamente, suspeita-se que a tinta amarela seca mais rápido do que a branca. Amostras foram obtidas para a medição dos tempos de secagem (em minutos), em condições reais das duas tintas:
c) Obtenha o para a variância do tempo de secagem de cada tipo de tinta.
Passo 1
Vamos começar pela tinta branca. Vamos calcular a variância amostral dela, começando calculando a média :
E agora podemos calcular por:
Passo 2
Como o nível de confiança pedido é de :
Agora vamos calcular nossos ², lembrando que . Primeiro o superior:
Procurando o valor desse cara aí na tabela:
E agora o inferior:
Procurando esse qui-quadrado na tabela:
Então o para a tinta branca, juntando tudo na fórmula, vai ser:
Passo 3
Agora vamos calcular para a tinta amarela. Primeiro a média amostral:
E agora podemos calcular por:
Passo 4
Agora vamos calcular nossos ², lembrando que e . Primeiro o superior:
Procurando o valor desse cara aí na tabela:
E agora o inferior:
Procurando esse qui-quadrado na tabela:
Então o para a tinta branca, juntando tudo na fórmula, vai ser: