Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 10

Entre 1.000 amostras, de 200 crianças cada uma, em quantas esperar-se-ia encontrar:

  1. menos de 40% de meninos;
  2. 53% ou mais de meninas.

Passo 1

Oi pessoal. Vamos pensar juntos neste exercício?!

Considerando que temos metade de meninos e meninas, então pelo enunciado temos os seguintes dados:

  • n = 200 ;
  • p = 0,50 ;
  • q = 0,50 .

Onde:

μ = n ∙ p = 200 ∙ 0,50 = 100

σ = n ∙ p ∙ q = 200 ∙ 0,50 ∙ 0,50 = 7,07

No item a) queremos saber quantas crianças se espera para menos de 40% serem meninos:

P x < 0 , 4 0

Sendo assim:

x = 0,40 ∙ 200 = 80

Com isso conseguimos calcular nosso valor z :

z = x - μ σ = 80 - 100 7,07 = - 2,83

Pela Tabela da Distribuição normal, temos:

P x < 0,40 = 0,0 023

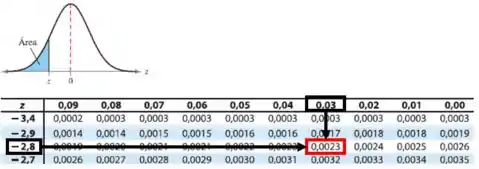
O número de meninos será:

0,0023 ∙ 1000 = 2

Passo 2

No item b) queremos saber quantas crianças se espera 53% ou mais de meninas:

P x < 0,40

Sendo assim:

x = 0 , 53 ∙ 200 = 106

Calculando o valor z :

z = x - μ σ = 106 - 100 7,07 = 0,85

Pela Tabela da Distribuição normal, temos:

P x ≥ 0 , 53 = 1 - P x < 0,53

P x ≥ 0,53 = 1 - 0 , 8 023 = 0,1977

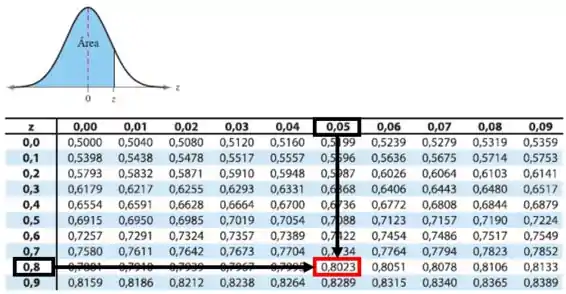
O número de meninas será:

0 , 1977 ∙ 1000 = 198

Tchau galerinha! Te espero em mais exercícios.

Resposta

  1. 2 meninos;
  2. 198 meninas.

Exercícios de Livros Relacionados

Numa indústria, 30% dos funcionários têm mais que 35a n o s . Selecionando-se, ao acaso e com reposição, 600 funcionários, qual a probabilidade de encontrarmos menos que 165 pessoas dessa faixa etária
Numa estrada, numa certa faixa de horários, passam em média 900 carros por hora, segundo uma distribuição de Poisson. Calcular a probabilidade de passarem, em 30 minutos, mais que 480c a r r o s .
Uma máquina automática embala em média 5,2 pacotes por minuto. Calcule a probabilidade de, em 1 hora de trabalho, ela embalar de 330a340 pacotes.
Um restaurante pode atender a 200 clientes por dia e, num certo dia, aceitou 220 reservas. A experiência mostra que 10% das pessoas que fazem reservas acabam não comparecendo. Calcular a probabilidade
Sabe-se que 16 pessoas, a cada 80 pessoas consultadas, são consumidores de certo produto. Entrevistando-se 400 pessoas, qual a probabilidade de encontrarmos:a) não mais que 90 pessoas que são consumid