Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 6.Exercícios propostos - Ex. 17

A tabela a seguir mostra o número de meses, de um total de 50, no qual ocorreram acidentes de trabalho numa empresa. Ajustar uma distribuição de Poisson para esses dados.

Passo 1

Olá galerinha, vamos resolver mais um exercício juntos? Então vamos lá!

Muitas vezes poderemos estar interessados em saber se uma determinada distribuição amostral segue um determinado modelo de distribuição teórica, tais como, a distribuição normal, binomial e Poisson. Dessa forma, levando em consideração se a distribuição amostral possui variável discreta ou contínua, se é um evento dicotômico ou raro, escolhemos a distribuição teórica que queremos ajustar.

O modelo de Poisson é dado por:

Onde representa o número de acidentes (0, 1, 2, 3 ou 4). E a média é estimada por meio da média amostral , que é obtida por:

Onde:

Logo:

Passo 2

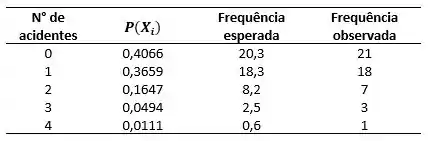
Então temos a seguinte distribuição de Poisson ajustada:

E as frequências esperadas () calculamos por:

Com isso, obtemos:

Tchau galerinha! Te espero em mais exercícios.

Resposta

Resposta no Passo 2.

Exercícios de Livros Relacionados

Ajustar uma curva normal às distribuições amostrais a seguir:

Comparar os resultados de uma distribuição Binomial com n = 10 e p = 1 / 2 , com uma distribuição normal com mesma média ( μ = n ∙ p ) e mesma variância ( σ 2 = n ∙ p ∙ q ). Verificar que a aproximaçã

Dada a distribuição abaixo, pede-se:ajustar uma distribuição Binomial aos dados;ajustar uma distribuição de Poisson aos dados, comparando com o ajustamento anterior.