10-75. Umestudo sobre economia de comhustivel foi conduzido em dois

automoveis alemāes. Mercedes e Volkswagen. Um veiculo de cada

marca foi selecionado, registrando-se a quantidade de milhas percorri

das com 10 tanques de combustível em cada carro. Esses dados (em

milhas por galao) sào mostrados a seguir:

a) Construa um gráfico de probabilidade normal para cada um dos con-

juntos de dados. Bascado nesses gráficos. é razoável considerar que

eles sejam retirados de uma população normal?

b) Suponha ter silodeterminado uue o menor valor observado dos dados

do Mereedes foi registrado erroneamente, sendo o valor corrcto ieual

a 24.6. Além disso. a menor valor observado dos dados do Volkswa-

gen foi também registrado erroneamente. sendo o valor correto igual

a 39.6. C'onsirua novamente gráficos de probabilidade normal para

cada um dos comjunlos de dados com os valores eorretos. Baseado

nesses novos gráficos. é razoável considerar que eles sejam retira.

dos de uma populacao normal?

c) Compare suas respostas dos itens (a) etb) e comente o efeito dessas

observaçues erradas na suposicão de normalidade.

d) Usando os dados eorretos do item (b) c um intervalo de contianca

. há evidencia quc contirme a afirmacão de quc a variabili-

dade no consumo de comhustível por milha seja maior para Volkswa.

gen do que para Mercedes?

e)Relaça o item íd) deste problema, usando um procedimento alequado

de teste de hipóteses. Voce obteve a mesma resposta que obteve

originalmente? Por que?

Amostra 1:

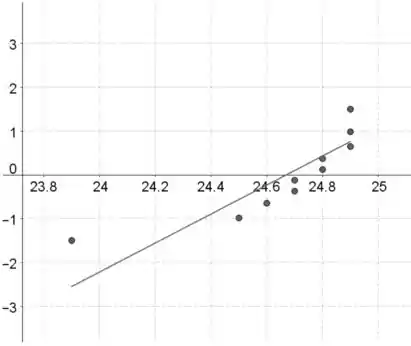
Amostra 2:

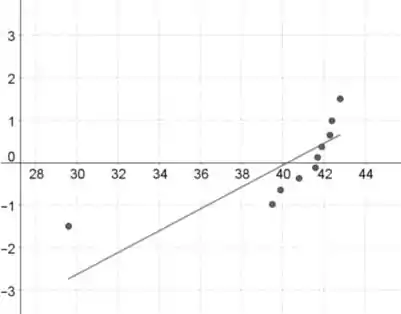
A suposição normal parece não estar satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é fortemente curvo, o que indica distribuição não normal.

Letra b:

A média é a soma de todos os valores dividida pelo número de valores:

A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:

Gráfico da probabilidade normal:

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.

Amostra 1:

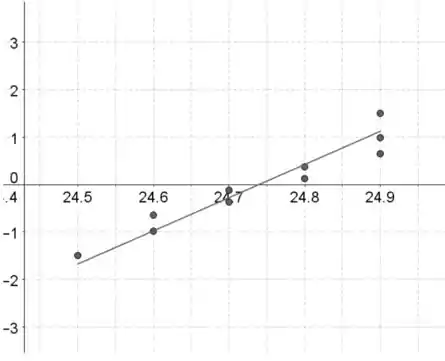
Amostra 2:

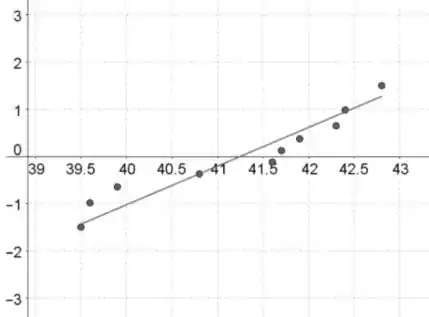
A associação normal parece satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente normal, o que indica que as distribuições são distribuídas aproximadamente normalmente

Letra c:

Os valores errados mudaram tanto a distribuição dos valores dos dados que a distribuição não parecia mais ser distribuída normalmente.

Letra d:

Determine os valores críticos usando a quarta tabela na tabela VI com e :

Os limites do intervalo de confiança são então:

Uma vez que o intervalo de confiança não contém 1, a variabilidade não parece ser a mesma em ambas as amostras e, portanto, há evidências suficientes para apoiar a alegação de variabilidade diferente.

Letra e:

Determine as hipóteses:

Calcule o valor da estatística de teste:

O valor crítico é dado na quarta tabela da tabela VI na linha com e na coluna com :

A região de rejeição contém todos os valores menores que 0.2481 e todos os valores maiores que 4.03.

Se o valor da estatística de teste estiver na região de rejeição, então rejeite a hipótese nula:

Há evidências suficientes para apoiar a alegação de variabilidade diferente. Obtemos a mesma conclusão porque o teste de significância e o intervalo de confiança descrevem os mesmos dados usando as mesmas estatísticas e distribuições de teste.