10-78. Dois diferentes medidores podem ser usados para medir a pro.
fundidade de um material tusado no banho de uma célula IHall. usada na
fundição de aluminio. Cada medidoré usado uma vez em 15 células pelo
mesmo operador.
a) Fstabeleça quaisquer suposiçoes necessánas para testar a afirmação
de que ambos os medidores produzem as mesmas leituras da pro-
fundklade media do material no banho. Verifique essas suposiçoes
nos dados que vocé tem.
b) Aplique um método estatistico apropriado para delerminar se os
dados contirmam a afirmação de que os dois medidores produzem
leituras diferentes da profundidade média do material do banho.
c) Suponha que se os dov medidores diferirem nas leituras da protun-
didkke media do material do banho por 1.65 poleeada. vamos que-
rer que a potencia do teste seja no minimo 0.8. Para r = 0.01. quan-
las células devem ser usadas?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dado:
Determine a diferença de valor para cada par de dados:
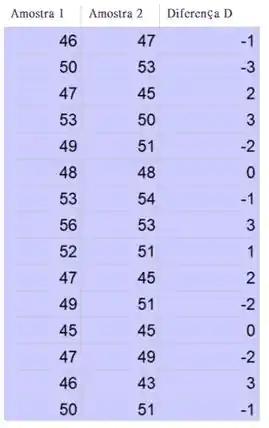
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividido por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Exigimos que as distribuições sejam distribuídas aproximadamente normalmente.
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
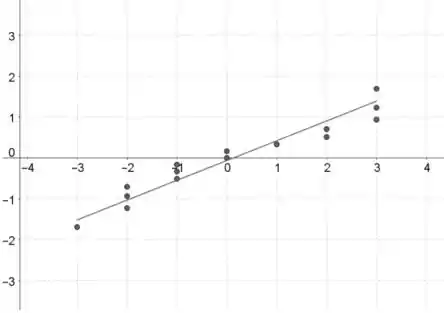
A suposição normal parece satisfeita. porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente linear, o que indica que as distribuições são aproximadamente distribuídas normalmente.
Passo 3
Letra b:
Determine as hipóteses:
Determine a estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t no na linha
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Há evidências suficientes para apoiar a alegação de que as leituras médias de profundidade no banho diferem.
Passo 4
Letra c:
Dados:
é o complemento da potência:
Fórmula do tamanho da amostra:
é a hipótese nula em
é a hipótese alternativa
Determine usando a tabela lll (procure 0.005 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Determine usando a tabela lll (procure 0.2 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Preencha os valores conhecidos na fórmula e avalie (arredonda para cima!):
Resposta
- Premissas satisfeitas
- Há evidências suficientes para apoiar a alegação de que as leituras médias da profundidade no banho diferem.