Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 79
10-79. Um artigo na revista Journal ofthe Enrironmenial Engineering
Dnison ("Distribution of Tonic Substances in Rners"-Distribuisao
de Substancias Tóxicas em Rios. 1982. Val. 108. pp. 6.39-649) investi
gou a concentraçae de varias substáncias oreánicas hidrofobieas no rio
Wolt no Tenneesse. Medidas de hexaclombenieno (HCBI em nanogra-
mas por litro são retiralas em diferentes profundidades a jusante de um lixào
ahandonado. Dados para duas protundidades sao mostrados a seguir:
a) Quais são as suposições requerklas para testar a alirmacão de que a
coneentração média le HCB éa mesma em ambas as proluklidades?
Verilique essas suposieoes para as quais vocé tem a informação.
b) Aplique um procedimento apropriado para delerminar se os dados
confirmam a afirmação do item (a).
c) Suponha quc a diferenea verdadeira nas concentracoes médias seja
2.0 nanogramas por litro. Para qual é a poténcia de um
teste estalistico para
d) Que tamanho de amostra seria requerido para detectar uma diferen-
ca de 1O nanograma por litro com se a potência tem de ser
no minimo 0.9?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividido por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Exigimos que as distribuições sejam distribuídas aproximadamente normalmente.
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
Passo 3
Amostra 1:
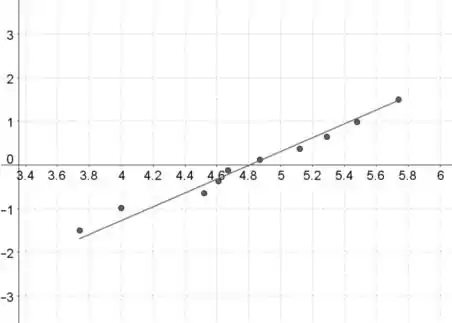
Amostra 2:
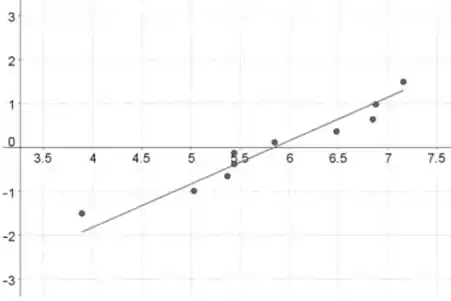
A suposição normal parece ser satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente linear, o que indica que as distribuições são aproximadamente normalmente distribuídas.
Passo 4
Letra b:
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o número inteiro mais próximo):
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t no na linha
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Há evidências suficientes para apoiar a alegação de que as concentrações médias de HCB são diferentes nas duas profundidades.
Passo 5
Letra c:
Dado:
O poder é a probabilidade de rejeitar a hipótese nula quando a hipótese alternativa for verdadeira.
Determine com usando a tabela V:
A diferença média da amostra correspondente é a diferença média da população (da hipótese) aumentada pelo produto do valor z e o desvio padrão:
O valor t é a diferença média da amostra diminuída pela diferença média da população (diferença média alternativa!), dividida pelo desvio padrão:
Determine a probabilidade de rejeitar a hipótese nula usando a tabela V com .
Passo 6
Letra e:
Dado:
é o complemento da potência
Fórmula do tamanho da amostra:
é a hipótese nula em
é a hipótese alternativa
Determine usando a tabela lll (procure 0.025 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Determine usando a tabela lll (procure 0.1 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Preencha os valores conhecidos na fórmula e avalie (arredonda para cima!):
Resposta
- Premissas satisfeitas
- Há evidências suficientes para apoiar a alegação de que as concentrações médias de HCB são diferentes nas duas profundidades.