Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 6º - Capítulo 8.Problemas - Ex. 48
Suponha E(X) = μ1, E(Y) = μ2, Var(X) = σ1², Var(Y) = σ2², Cov(X, Y) = σ12. Então, o coeficiente de correlação entre X e Y é dado por
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e dar o coeficiente de correlação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar a função.
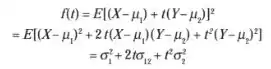
Como ela é sempre positiva ou nula, quaisquer que sejam os parâmetros σ1², σ2² e σ12. Sendo um polinômio do segundo grau em t, o seu discriminante deve ser negativo ou nulo, isto é,
Passo 3
O que satisfaz à relação:
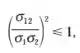
Que implica
Resposta
Exercícios de Livros Relacionados
A distribuição conjunta das variáveis aleatórias contínuas X, Y e Z é constante ao longo da região x 2 + y 2 ≤ 1 ,0z4 . Determine o seguinte: P ( X 2 + Y 2 ≤ 0.5 ) P ( X 2 + Y 2 ≤ 0.5 , Z2 ) A função
Determine o valor de c, tal que a função f ( x , y ) = c x 2 y , para 0x3 e 0y2 , satisfaça as propriedades de uma função de uma função densidade de probabilidade conjunta.Determine o seguinte: P ( X1
Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjunta: determine o seguinte:Determine o seguinte:
O Torque requerido para remover parafusos e uma placa de aço é classificado como alto, moderado ou baixo. Historicamente, a probabilidade de uma classificação alta, moderada ou baixa é 0.6,0.3 ou 0.1,
A porcentagem de pessoas que tomam o medicamento contra reumatismo, que só prefere colaterais severos, moderados ou menores, é igual a 10,20 e70%, respectivamente. Considere que as pessoas reagem de f