11-11. Um motor de um foguete é fabricado ligando-se dois tipos de
propelentes: um iniciadore um mantenedor. Pensa-se que a tensäo cisalhante
na ligação, y, seja uma funcão linear da idade do propelente, a, quando o
motor for moldado. Vinte observações sào mostradas na tabela seguinte.

a) Desenhe um diagrama de dispersào dos dados. Um modelo de re-
gressão linear simples parece apropriado aqui?
b)Pelo método dos minimus quadrados. encontre as estimativas da
inclinação c da interseção para o modelo de regressão lincar simples.
Enconire uma estimativa para or.
c) Estime a tensão média cisalhante de um motor feito a partir de um
propelente com 20 seinanas.
d)Obtenha os valores ajustados. , que correspondein a cada valor
ohservado y. Plote versus v, e comente o que esse gráfico parece-
ria se a relação lincar entre a tensão cisalhante e a idade fosse per-
feitamente deterministica (sem erro). Esse gráfico indica que a ida-
de seja uma escolha razoável de regressor nesse modelo?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
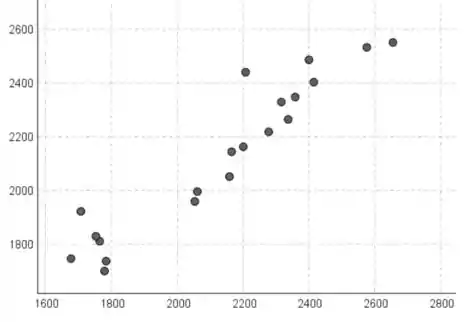
Letra a:
x está no eixo horizontal e y está no eixo vertical.

Isto parece razoável usar um modelo de regressão linear simples, porque não há curvatura forte no gráfico de dispersão.
Passo 2
Letra b:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 3
Letra c:
Substitua x na linha de regressão de mínimos quadrados por 20 e avalie:
Passo 4
Letra d:
Os valores y estão no eixo horizontal e os valores ajustados estão no eixo vertical.
Resposta
- Razoável
- Sim