Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 68
11-68. Os dados mostrados a seguir expressam X- o contcúdo de água
na neve. em l: de abril. c Y - o campo fem polcgadas). de abril a julho.
nas encostas do Snake River em Wyoming. de 1919 a 1935. (Os dados
foram retiradus de um artigo cm Reseurch Notes. Vol. 61. 1950. Esta-
cao Experimental da Floresta Situada na Faixu Noroeste do Pacítico -
Pucijuc Northwest Forex Range Experiment Station, Oregon.)
a) Estime a correlação cntre Ye X.
b) Teste a hipótese de que p = O usando a - 0.05.
c) Ajuste um modelo de regressão linear simples e teste a significância
da regressão usando a =0.05. Que conclusoes voce pode tirar? Como
está relacionado o teste para a significáncia da regressao ao leste para
p no item(b)?
d) Analise os residuos e comente a adequação do moxdelo.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Dados:
Letra a:
Encontre como foi feito na tabela abaixo.
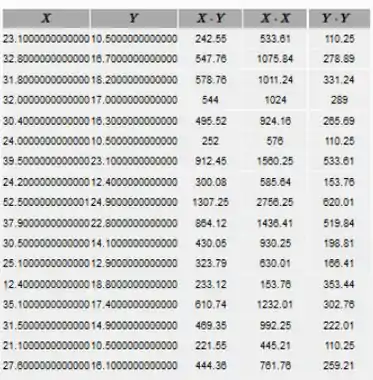
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 2
Letra b:
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, rejeita a hipótese nula:
Existem evidências suficientes para apoiar a afirmação de que existe uma correlação linear.
Passo 3
Letra c:
O teste de significância da regressão terá sempre o mesmo resultado que o teste em porque ambos os testes levam ao mesmo valor t, e ambos os testes têm os mesmos graus de liberdade.
Existem evidências suficientes para apoiar a afirmação de que a regressão é significativa.
Encontre como foi feito na tabela abaixo.
Agora, encontre a soma de cada coluna para obter:
E então, use as seguintes equações para encontrar a e b:
Daí, substitua a e b na fórmula da equação de regra
Passo 4
Letra d:
O valor da estatística de teste é
Determine a probabilidade correspondente (valor P) usando a tabela V com :
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Não há evidência suficiente para apoiar a alegação de que a correlação é diferente de 0.5.
Resposta
- Existem evidências suficientes para apoiar a afirmação de que existe uma correlação linear.
- Há evidências suficientes para apoiar a alegação de que a regressão é significativa.
- Não há evidência suficiente para apoiar a alegação de que a correlação é diferente de 0.5.