Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 71
11-71. Em um artigo na revista IEEE Transactions on Inirumentation
and Measuremenr (2001. Vof. 50.pp. 986 990). pesquisadores estuda-
ramos efeitos de reduzir. por meios eletronicos, a perda de corrente em
um núcleo magnético. Realizando um expenmento emparelhado, eles
mediram a corrente em um enrolamento magnético com e sem a cletro-
nica. sendo os dados para o caso sem eletrônica apresentados na tabela
a seguir.
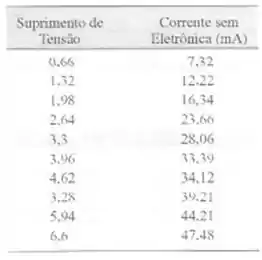
a) Faça um gráfico e ajuste uma linha de regressão para prever a cor-
rente sem cletronica em função do suprimento de voltagem. Há uma
regressao signifieativa para a = 0.057 Qual é o valor P'
b) Estime o coeliciente de correlação.
c) Teste a hipotese de que p - O contra a altemativa p 0 usando a -
0.05. Qual é o valor P?
d) Calcule um intervalo de conliança de 95% para o cocficiente de
correlacao.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Dados:
Letra a:
A tensão de alimentação está no eixo horizontal e a corrente sem eletrônica está no eixo vertical.
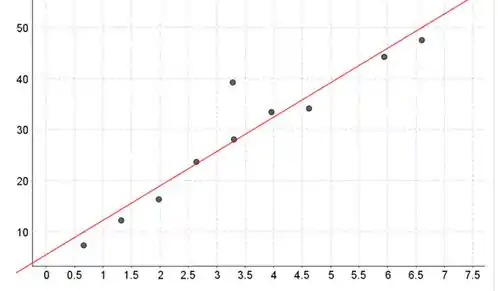
Passo 2
Determine a equação de regressão de mínimos quadrados:
Encontre como foi feito na tabela abaixo.
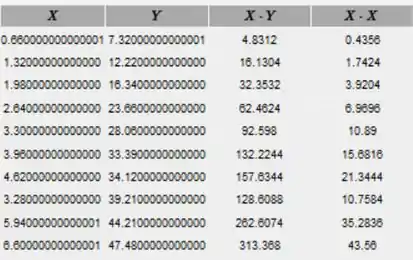
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Substitua a e b na fórmula da equação de regressão:
Passo 3
Determine o coeficiente de correlação linear r:
Encontre como foi feito na tabela abaixo.
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 4
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
Passo 5
Letra b:
Encontre como foi feito na tabela abaixo.
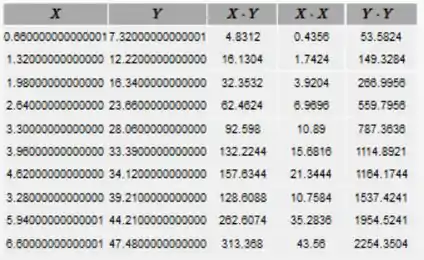
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 6
Letra c:
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
Passo 7
Letra d:
Para o nível de confiança , determine usando a tabela III (procure 0.025 na tabela, o valor z é então o valor z encontrado com sinal oposto):
Os limites do intervalo de confiança para o coeficiente de correlação são então:
Resposta
- . Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
- Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.