Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 9
11-9. Um artigo em Wear IVol. 152, 1992. p. 171-181) apresenta da
dos sobre o desgaste abrasivo do aco doce e a viscosidade do oleo. Dados
representativos são moslrados na tabela a seguir. com x = viscosidade
do ólco c y = volume desgastado
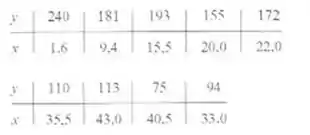
a) Construa um diagrana de dispersão dos dados. Um modelo de re-
gressão lincar vimple» parece ser plausivel?
b) Ajuste um modelo de regressáo linear simples usando o método dos
minimos quadrados. Encontre uma cstimativa para
c) Preveja o desgaste abrasivo. quando a voeosidade for x - 30.
d) Obtenha o valor ajustado de y quando x-22.0 c calcule o residuo
correspondente.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Letra a:
x está no eixo horizontal e y está no eixo vertical.
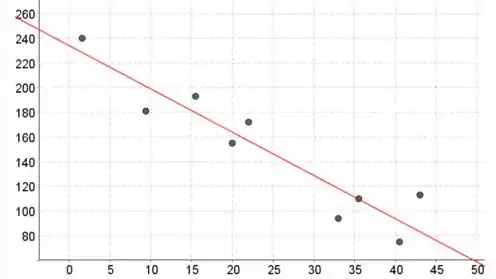
Isto parece razoável usar um modelo de regressão linear simples, porque não há curvatura forte no gráfico de dispersão.
Passo 2
Letra b:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 3
Letra c:
Substitua x na linha de regressão de mínimos quadrados por 30 e avalie:
Passo 4
Letra d:
Substitua x na linha de regressão de mínimos quadrados por 22.0 e avalie:
O resíduo é o valor real diminuído pela quantidade prevista:
Resposta
- Razoável