Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 16.Problemas - Ex. 27
Num experimento foram aplicadas três doses diferentes de insulina em coelhos e foram observadas quedas na quantidade de açúcar no sangue (variável ) depois de determinados
Períodos. Nesse tipo de experimento, é usual admitir-se que a relação entre queda de açúcar e o logaritmo da dose da insulina é linear.
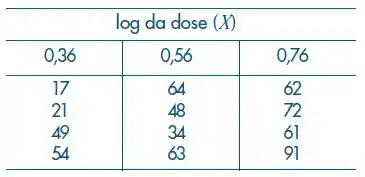
São dados:
Faça um estudo completo sobre o ajuste do modelo a esses dados.
Passo 1
Neste exercício, vamos inicialmente encontrar a reta de mínimos quadrados , em que:
Portanto, .
Vamos construir a tabela ANOVA para o modelo em questão.
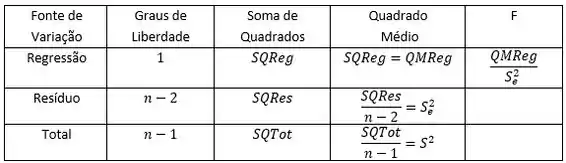
Neste caso, teremos:
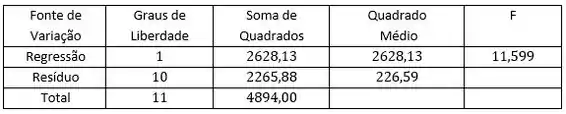
Resposta
Com o alto valor encontrado para a estatística , concluímos pela rejeição de Dessa forma, a log da dose de insulina ajuda a prever a queda na quantidade de açúcar no sangue.
Exercícios de Livros Relacionados
12-62. Ajuste um moxlelo à resposta PASSO nos dados de tratamentotérmico do Exercicio 12-8. usando noves regressores AICLO X CONCCARBex.-CICL.ODIFXCONCCARBDIF.a) Calcule R para esse modclo e compare-o
12-63. Considere os dados HFE dos semicondutores do Exereicio 12-7.a) Plote os resáluos kesse modelo contra y. Comente a informacao quepode ser obtida a partir desse gráfico.b) Qual é o valor de R par
12-65. Os elementos da diagonal da matriz chapéu são freqüentementeusados para denotar alavancagem ileverage) - ou seja. um ponto quenào é usual em sua localizacão no espaço A e que pole ser intluente
12-67. Considere os seguintes dados. que resultam de um cxpcrimentopara determinar o cteito de x = tempo de teste, em horas. em uma tem-pcratura particular, sohre y - mudança na viscosidade do óleo:Aj
12-68. O,dados mostrados a seguir foram coletados durante um expe-rimento para determinar a variação na eficiência de impulsão (y. cmporcentagem) à medida que varia o ângulo de divergencia de um bocal