Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 12.Exercícios - Ex. 88
12-88. Os dados mostrados na Tabela 12-21 representam a impulsão de
um motor de um avião a jato O) e scis candidatos a regressor: xi=
velocidade principal de rotação. x, = velocidade seeundária de rota-
çáo. x, t vazão de combustível. x, - pressáo. s. = lemperatura de
exaustão c x, = lemperatura ambiente no momento do teste.
a)Ajuste um modelo de regressäo lincar múltipla. usando como regres-
sores.x
vazāo de combustível. x. = pressáo e x, = temperatura
de cxaustão.
b) Teste a significância da regressão usando = 0.01. Encontre o va-
lor P para esse teste. Quais são suas conelusòes?
c)Encontre a estatísticaf de leste para cada regressor.Usandoa-0.01.
explique cuidadosamente a conclusáo que vocé pexde tirar dessas
cstatisticas.
d)Encontre Re e a estatistica ajustada para esse modelo.
c)Construa um gráfico de probabilidade normal dos resíduos e inter-
prete esse gráfico.
f) Plote os residuos contra ý. Há alguma indicação de desigualdade de
variância ou não-linearidade?
g)Plote os resíduos contra.x, Há alguma indicação de näo-linearidade?
h) Preveja a impulsão para um motor no qual .x - 28.900. x=170c
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Letra a:
Eu ajustei o modelo linear usando os 3 regressores mencionados:
Passo 2
Letra b:
Sabemos que a estatística de teste F deve ser calculada da seguinte maneira.
Nós sabemos que:
Vamos lembrar que:
Então,
Calculamos que:
Portanto, a estatística F é
O valor p para o teste de significância da regressão é então obtido como
A hipótese é, portanto, rejeitada, a regressão é significativa.
Passo 3
Letra c:
Precisamos calcular as estatísticas de teste para os coeficientes de regressão até .
Calcule:
Os valores p correspondentes para os testes t são então facilmente obtidos:
A hipótese nula de o coeficiente ser 0 é rejeitada (sob para o caso das variáveis, mas a variável não contribui para o modelo.
Passo 4
Letra d:
Calcule o coeficiente de determinação e seu valor ajustado:
Passo 5
Letra e:
Aqui apresentamos o gráfico de probabilidade normal dos resíduos. Os dados são geralmente disperso ao redor da linha, mas observamos um certo padrão ondulado que não é bom.
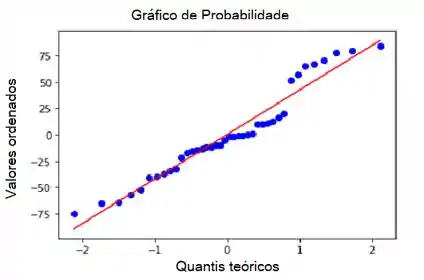
Passo 6
Letra f:
No gráfico residual abaixo, não há indicação de desigualdade de variância ou não linearidade:
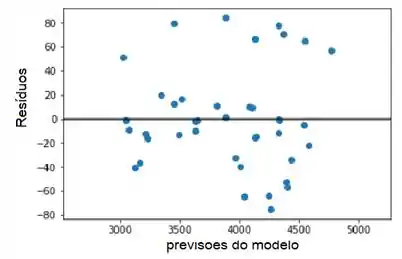
Passo 7
Letra g:
Aqui vemos o gráfico de resíduos versus o regressor . Não há indicação de não linearidade.
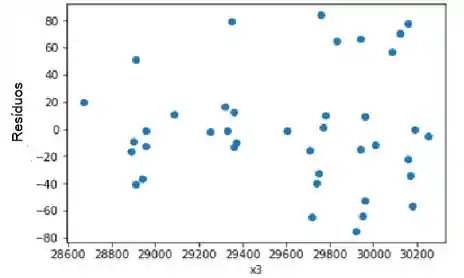
Passo 8
Letra h:
Conecte o ponto de dados na linha do modelo para obter a previsão:
Resposta
- Apenas não contribui. Outros são significativos.
- Ver resolução
- Ver resolução
- Ver resolução