Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 108
9.108. A torça média de remoção de um adesivo usado na fabricação
de um conector para uma aplicação em um motor de automóvel deve
ser no mínimo igual a 75 libras-torça. Esse adesivo será usado, a menos
que haja uma forte evidência de que a força de remoção não encontre
csse requerimento. Um teste de uma hipótese apropriada deve ser con-
duzido com tamanho de amostra n
10 c a = (0,05. Considere que a
força de remoção seja normalmente distribuida e que o não se ja conhe-
cido.
(a) Se o desvio-padrao verdadeiro for r - 1. qual é o risco de que o
adesivo seja julgado accito quando a força verdadeira média de re-
moção for somente 73 libras-força? Somente 72 lihras-força?
(b) Que tamanho da amostra é requerido para fornecer 90G de chance
de detectar que a média verdadeira seja somente 72 libras força quan-
do o = 1?
c) Refaça os itens (a) e (h) supondo que o – 2. Qual o impacto que o
aumento do valor de or causa nas respostas que voce obteve?
Passo 1
Faaaala aí,
Vamo aprender uma questão aqui?
Vamo!
Estamos interessados em testar:
Contra
com e . Suponha que a força média de remoção é normalmente distribuída e não é conhecido.
Passo 2
Letra a:
Quando calculamos erro tipo II, às vezes é mais conveniente usar as curvas de característica de operação (OC) nos gráficos VIIa ou VIIb do Apêndice. Essas curvas representam em relação a um parâmetro para vários tamanhos de amostra . O parâmetro é definido como
Se o verdadeiro desvio padrão for e a verdadeira força média de remoção for apenas libras, então, da Equação (1)
Então, a partir dos gráficos do Apêndice, obtemos
Se a verdadeira força média de remoção for apenas libras, então da Equação (1):
Então, a partir dos gráficos do Apêndice, obtemos
A probabilidade de que o adesivo seja considerado aceitável, quando a verdadeira força média de remoção é apenas ou libras é 0.
Passo 3
Letra b:
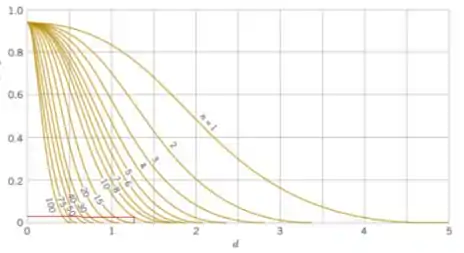
Se houver 90% de chance de detectar que a média verdadeira é apenas libras quando , então
E
Então, a partir dos gráficos do Apêndice, obtemos
Veja a figura:
Passo 4
Letra c:
Se o verdadeiro desvio padrão for e a verdadeira força média de remoção for apenas libras, então, da Equação (1)
Então, a partir dos gráficos do Apêndice, obtemos
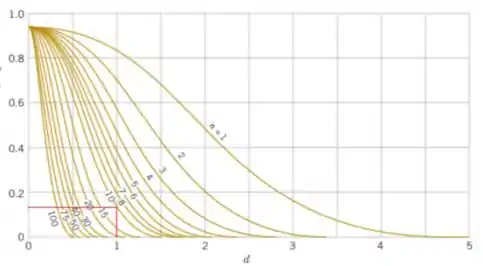
Se a verdadeira força média de remoção for apenas libras, então, da Equação (1)
Então, a partir dos gráficos do Apêndice, obtemos
Se o desvio padrão aumentar, então será aumentado.
Resposta
- Se , então o erro tipo II é . Se , então o erro tipo II é .
- O tamanho da amostra é
- Se , então o erro tipo II é . Se , então o erro tipo II é .