Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 39
Os dados a seguir representam os tempos de duração de filmes produzidos por duas indústrias cinematográficas:
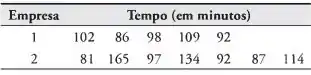
Teste a hipótese de que o tempo médio dos filmes produzidos pela empresa 2 excede o tempo dos filmes da empresa 1 em dez minutos, contra a alternativa unilateral de que a diferença é menor que dez minutos. Use um nível de significância de 0,1 e assuma que as distribuições dos tempos são aproximadamente normais com variâncias desiguais.
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”
Bora empurrar e macetar essa questãozinha comigo agora
Na pergunta, são fornecidos os dados sobre os tempos de exibição dos filmes feitos por duas empresas.
O pesquisador deseja verificar se a diferença entre o tempo médio de execução da empresa 2 e da empresa 1 é menor que 10 ou não.
As hipóteses nulas e alternativa para o cenário fornecido podem ser definidas como:
Aqui, a hipótese nula, é a hipótese alternativa.
O tempo médio de execução da empresa 2 e da empresa 1 são representados por respectivamente.
Aqui, a hipótese nula indica que a diferença entre o tempo médio de execução da empresa 2 e da empresa 1 é 10.
A hipótese alternativa indica que a diferença entre o tempo médio de execução da empresa 2 e da empresa 1 é menor que 10.
Passo 2
As etapas abaixo mencionadas podem ser seguidas no software Minitab, para poder obter o resultado do teste
Passo 1: Insira os dados na planilha do Minitab.
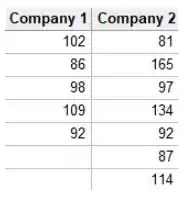
A média e o desvio padrão para empresa 1, são calculadas da seguinte maneira
Desvio padrão da amostra
A média e o desvio padrão pra a empresa 2 é
Desvio padrão da amostra
Passo 3
A estatística de teste é calculada da seguinte maneira
Assim o valor da estatística de teste 1 é .
Passo 4
Os graus de liberdade são calculados para o método de variância desigual da seguinte maneira
Portanto, o valor de p com 7 graus de liberdade do teste t de cauda esquerda é calculado da seguinte forma
Como o p -valor obtido é menor que 0,1 nível de significância, a hipótese nula será rejeitada.
Portanto, a diferença entre o tempo médio de execução da empresa 2 e da empresa 1 é menor que 10.
“Faça seus medos terem medo de você”
Resposta
Portanto, a diferença entre o tempo médio de execução da empresa 2 e da empresa 1 é menor que 10.