Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 60
9-60. O Exercicio 6-22 torncceu dados sobre as alturas de estudantes femininas de engenharia em SU.
(a) Você pode sustentar a afirmação de que a altura média de estudantes femininas de engenharia cm ASU é no minimo 65 polegadas? Use a = 0,05. Encontre o valor P.
(b) Verifique a suposição de normalidade.
(c) Calcule a poténcia do teste. se a altura média verdadeira for 62 polegadas.
d) Que tamanho da amostra seria requerido para detectar uma altura media verdadeira de 64 polegadas. se quisé\'ssemos que a potëncia do teste fosse no mínimo 0.8?
Passo 1
Oi oi gente, tudo bom com vocês?
Vamos fazer essa questão aqui de um jeito bem passo a passo pra facilitar a vida de todo mundo!Boraaa
Nos é dado que:
Letra a:
A média é a soma de todos os valores divididos pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor do que o nível de significância, a hipótese nula é rejeitada.
Não há evidências suficientes para apoiar a alegação de que a altura média das alunas de engenharia na ASU é de pelo menos 65 polegadas.
Passo 2
Letra b:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem valores de dados, os valores normais padronizadas são os valores z na tabela III correspondentes a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde à segunda menor pontuação de dados e assim por diante.
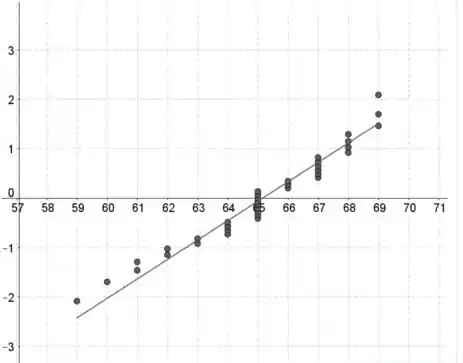
A suposição Normal parece satisfeita, porque o gráfico de probabilidade normal não parece conter uma forte curvatura..
Passo 3
Letra c:
A potência é a probabilidade de rejeitar a hipótese nula quando a hipótese alternativa é verdadeira.
Determine o valor t correspondente a e na tabela V:
A média da amostra correspondente é a média da população (da hipótese) aumentada pelo produto do valor z e do desvio padrão:
O valor t é a média da amostra diminuída pela média da população (média alternativa), dividida pelo desvio padrão:
Determine a probabilidade de rejeitar a hipótese nula usando a tabela V, que é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Passo 4
Letra d:
Determine o valor t correspondente a uma potência de e na tabela V:
Determine o valor t correspondente a e na tabela V:
A média da amostra correspondente é a média da população (da hipótese) aumentada pelo produto do valor z e o desvio padrão:
O valor t é a média da amostra diminuída pela média da população (média alternativa). dividido pelo desvio padrão:
Esses valores devem ser iguais aos valores t correspondentes à potência:
Subtraia de cada lado:
Divida cada lado por :
Eleve ao quadrado cada lado e arredondado para o número inteiro mais próximo, temos:
Resposta
- Não há evidências suficientes para apoiar a alegação de que a altura média das alunas de engenharia na ASU é de pelo menos 65 polegadas.
- Satisfaz