Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 51
9-51.Uim artigo de 1992 na revista Journal ofthe American Medical Asso-
ciation("A Critical Appraisal of 98,6 Degrees F.the Upper Limit of the
Normal Body Temperature,and Oiher lxgacies ef Carl Reinhold August
Wilerfich"-Um Laudo Critico de 98.6F.o Limite Superior da Tem-
peratura Normal do Corpo c Outros Legados de Carl Reinhold August
Wurlerlich reportou temperatura do corpo.genere taxa do coracao para
varias pessoas.As temperaturas do corpo para 25 mulheres foram:97.8:
97.2:97.4:97.6:97,8:97.9:98.0:98.0:98.0:98,1:98.2:98,3:98.3:98.4;
98.4:98.4:98.5:98.6:98.6:98.7:98.8:98.8:98.9:98.9c99.0.
（a)Teste as hipoteses Hp=98.6 versus H:u98.6.usando=
0.05.Encontre o valor P.
（b)Verifique a suposicao de que a temperatura do corpo feminino e
normalmente distribuida.
（c)Caleule a potencia do teste se a temperatura media verdadeira do
corpo feminino e tao alta quanto 98.0.
（d)Que tamanho da amostra seria requendo para detectar uma tempe-
ratura media verdadeira do corpo feminino tao baixa quanto 98.2.
se quisessemos que a poteneia do teste fosse no miniio 0.97
（C)Explique como a questao no item(a)podena ser respondida.constmin-
do u intervalo bilateral para a temperatura media do corpo feminino.
Passo 1
A média da amostra é
e o desvio padrão é:
O valor P para o teste contra a alternativa de dois lados é a probabilidade acima de mais a probabilidade abaixo. Porque a distribuição t é simétrica em torno de zero, uma maneira simples de escrever isso é
onde usará a estatística de teste
Passo 2
Letra a:
Precisamos testar
Contra
usando
O teste de estatística é
Sabemos que , então, da Tabela V do Apêndice, obtemos
Se então, falhamos em rejeitar .
Portanto,
e concluímos que é verdadeiro.
Agora, da Equação (1), obtemos
Da Tabela V do Apêndice nós sabemos
Portanto,
Então, o valor P é
Passo 3
Letra b:
Um gráfico de probabilidade normal é um método gráfico para determinar se os dados da amostra estão em conformidade com uma distribuição normal hipotética com base em um exame visual subjetivo dos dados.
Para construir um gráfico de probabilidade, as observações na amostra são classificadas primeiro da menor para a maior. Isso é, a amostra é organizado como onde é a menor observação, é a segunda menor observação e assim por diante com a maior. A frequência cumulativa para observação é
Uma probabilidade normal é construída em eixos ordinários traçando as pontuações normais padronizadas contra onde as pontuações normais padronizadas satisfazem
Nos eixos horizontais estão os valores . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados desviarem significativamente de uma linha reta, o modelo hipotético não é apropriado. Da maneira descrita anteriormente, construímos um gráfico de probabilidade normal com base nas observações 97,8, 97,2, 97,4, 97,6. 97,8, 97,9. 98,0, 98,0. 98,0, 98,1. 98,2, 98,3, 98,3, 98,11, 98,4, 98,4, 98,5, 98,6, 98,6, 98,7, 98,8, 98,8. 98,9, 98,9 e 99,0.
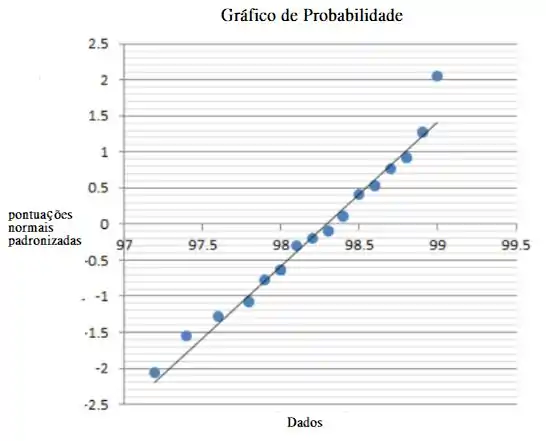
O gráfico de probabilidade normal não contém curvatura forte e o padrão é quase linear, então podemos concluir que os valores dos dados são distribuídos aproximadamente normalmente.
Passo 4
Letra c:
Quando o valor verdadeiro da média é , a distribuição de é chamada de distribuição t não central com grau de liberdade e parâmetro de não centralidade . O erro tipo II da alternativa de dois lados seria
onde denota a variável aleatória t não central, ou seja,
Encontrando a probabilidade de erro do tipo II para o teste t envolve encontrar a probabilidade contida entre dois pontos da distribuição t não central. Este problema já foi resolvido, e os resultados são resumidos em uma série de curvas nos Gráficos do Apêndice VIIe, VIIf, VIIg e VIIh. As curvas são fornecidas para alternativas bilaterais nos Gráficos VIIe e VIIf. Nesses gráficos, o fator d é definido como
Para a alternativa unilateral ou usamos os gráficos VIIg e VIIh.
Nós vemos que d depende do parâmetro desconhecido . Podemos evitar essa dificuldade de várias maneiras. Em alguns casos, poderíamos usar a variância da amostra para estimar um .
Nós sabemos que a verdadeira temperatura média interior chega a 98.0. Então,
Referindo-nos às curvas características de operação no Apêndice Gráfico VIIe (para ) com e , descobrimos que , aproximadamente.
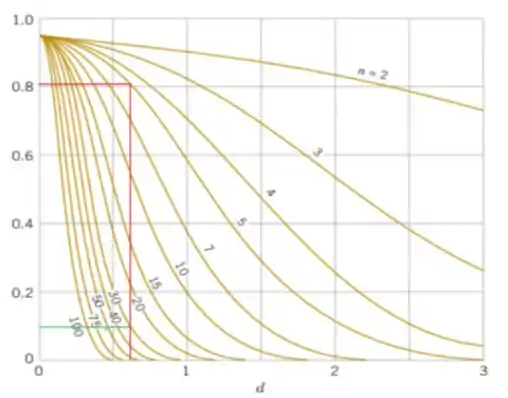
Então, a potência do teste é
Passo 5
Letra d:
Queremos a potência do teste a ser pelo menos e média da amostra verdadeira , então (ver figura anterior, linha verde). Em seguida, vemos que o tamanho da amostra é
Passo 6
Letra e:
Um IC bilateral de na média é
Portanto, um IC bilateral de 95% na média é
Se testarmos
Contra
Então deixamos de rejeitar porque 98.6 não está em um IC de