Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 87
9-87. Seja Xo número de talhas ohservadas em uma grande serpentina
de aco galvanirado. Setenta e cinco serpentinas sáo inspecionadas eos
seguintes dados foram observados para os valores de X.
（a) A suposição de distribuição de Poisson parece apropriada como um
modelo de probabilidade para esses edacdos? Use a - 0.01.
（b) Calcule o valor P para esse teste.
Passo 1
Faaaala aí,
Vamo aprender uma questão aqui?
Vamo!
A média é a soma de todos os valores divididos pelo número de valores:
A probabilidade pode ser determinada usando a distribuição de Poisson com média
:
Vamos avaliar em :
A hipótese nula afirma que as proporções da população são todas iguais:
Passo 2
A hipótese alternativa afirma o oposto da hipótese nula:
Determine as frequências observadas .
As frequências esperadas são o produto do tamanho da amostra n e as probabilidades .
Os subtotais do qui-quadrado são as diferenças de quadrados entre as frequências observadas e esperadas, divididas pela frequência esperada.
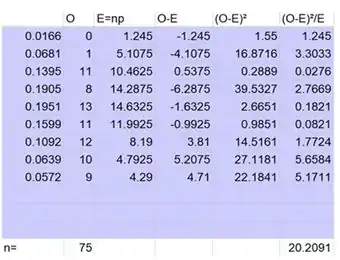
O valor da estatística de teste é então a soma dos subtotais qui-quadrado:
O valor P é a probabilidade de obter o valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela C contendo o valor na linha :
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Não há evidência suficiente para rejeitar a afirmação da distribuição de Poisson.
Resposta
- Não há evidência suficiente para rejeitar a afirmação da distribuição de Poisson.