12-63. Considere os dados HFE dos semicondutores do Exereicio 12-7.
a) Plote os resáluos kesse modelo contra y. Comente a informacao que
pode ser obtida a partir desse gráfico.
b) Qual é o valor de R para esse modelo?
c) Reajuste o modelo usando logi HFE} como a variável de resposta.
d)Plotc os residuos contra valores previstos de log(HFE) para o mo-
delo do item (c). Isso formeee qualquer informação acerca de qual
modelo seja preterivel?
e) Plote os resituos do moxielo do item idi contra o regressor x.. Co-
mente esse gratico.
f) Reajuste o modelo para log(liFE) usando s.x.e l/x, como os re-
gressores. Comente o cfeito dessa mudança no modelo.
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Neste exercício, você deve usar os dados fornecidos no exercício 12.7.
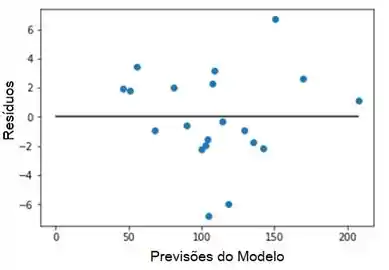
Letra a:
Plote os resíduos versus as previsões do modelo. O gráfico sugere que o modelo está bom - a variância é geralmente homogênea no tempo e os resíduos são dispersos aleatoriamente em torno do eixo horizontal.
Passo 2
Letra b:
Para calcular o coeficiente de determinação precisam ser obtidos. Portanto:
Finalmente,
Concluímos que cerca de 99,37% da variabilidade total é explicada pelo modelo.
Passo 3
Letra c:
Agora ajusto o novo modelo linear. Usando o logaritmo natural dos dados de resposta como a nova resposta. O melhor ajuste é a seguinte linha:
Passo 4
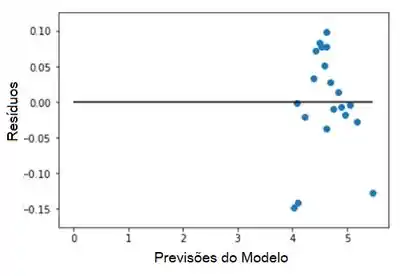
Letra d:
Plote os resíduos em comparação com as previsões do modelo para o modelo encontrado na parte anterior. O gráfico parece um tanto piramidal.
Pode-se preferir o modelo original.
Passo 5
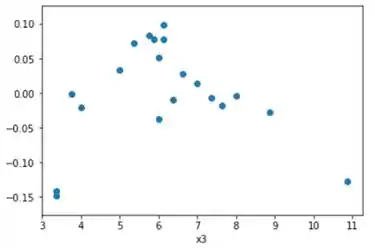
Letra e:
Nesta parte, plotamos os resíduos do segundo modelo (logaritmo natural) versus a variável de regressor . O gráfico não é desejável.
Existe um forte padrão piramidal.
Passo 6
Letra f
Agora, reajustamos o modelo de logaritmo natural com a variável de regressor de mudança (faça o inverso). O seguinte modelo é obtido:
Este modelo é melhor do que o anterior, como pode ser visto no gráfico residual versus regressor

Resposta
- Ver resolução
- Ver resolução
- Ver resolução