Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.Revisão - Ex. 33
De uma amostra aleatória de domicílios, listamos o número de aparelhos de televisão. Encontre a média e o desvio padrão amostral dos dados.
Números de televisores 0 1 2 3 4 5
Números de domicílios 1 8 13 10 5 3
Passo 1
Observando os dados fornecidos identifica-se que se trata de uma questão de média ponderada, onde seu cálculo é dado por:
Ou seja, vamos calcular o número médio de TVs por domicílio, sendo assim x é o número de televisores, e f (os pesos, ou quantas vezes o número de TVs se repete) é dado pelo número de domicílios.
Passo 2
A média é calculada da seguinte forma:
Passo 3
O desvio padrão exige um cálculo mais longo, pois é necessário calcular o somatório dos quadrados dos desvios médios de todos os termos.
Seguindo alguns passos, de forma metódica, para não ocasionar em erros, fazemos:
Passo 3.1: O valor de cada x – a média obtida:
0 – 2,475 = – 2,475; 1 – 2,475 = – 1,475; 2 – 2,475 = – 0,475; E assim por diante para os 6 valores tabelados.
Passo 3.2: Eleva-se cada resultado ao quadrado:
(- 2,475)2 = 6,125625; (- 1,475)2 = 2,175625; E assim por diante para os 6 valores obtidos anteriormente no passo 3.1.
Passo 3.3: Multiplica-se cada resultado obtido no passo 3.2 pelo valor respectivo de f da tabela dada no enunciado.
6,125625 . 1 = 6,125625; 2,175625 . 8 = 17,405; E assim por diante para os 6 valores.
A tabela a seguir expõe os resultados:
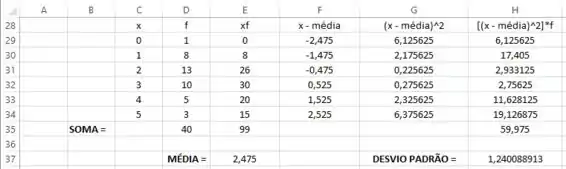
Passo 4
Usando o somatório obtido (célula H35) e a equação , sendo que n é o somatório dos valores de f, teremos que o desvio padrão da amostra dada é calculado da seguinte forma:
Resposta
Média = 2,475
Desvio padrão = 1,24