70.
a.
No Exercício 66, qual a mediana do tempo de vida das válvulas? [Sugestão: use a Expressão (4.12).]
b.
No Exercício 68, qual é a mediana do prazo de retorno?
c.
Se X tiver uma distribuição de Weibull com a fdc da Expressão (4.12), obtenha uma expressão geral para o (100p)ésimo percentil da distribuição.
d.
No Exercício 68, a empresa deseja recusar devoluções após t semanas. Para que valores de t apenas 10% de todas as devoluções serão recusadas?
Passo 1
Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.
Uma variável aleatória X tem distribuição de Weibull com parâmetros () se a fdp de X for:
Resposta
- P
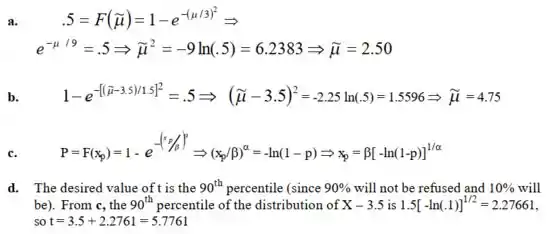
d. O valor desejado de t é o percentil 90 (já que 90% não serão recusados e 10% serão). De c, o percentil 90 da distribuição de

Até a próxima!!!