Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 23
Aplique o método de Tukey modificado para os dados do Exercício 22, a fim de identificar diferenças significativas entre os
Passo 1
O seguinte é necessário para entender como calcular as quantidades mencionadas e necessárias.
Tamanhos de amostra desiguais
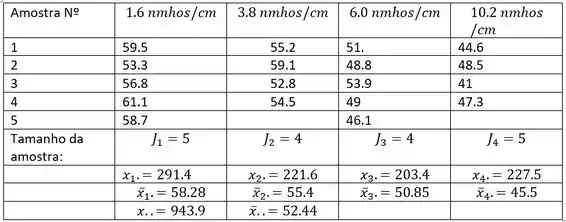
Seja sejam os tamanhos de amostra dos tratamentos I e sejam ser o número total de observações. Denote com
A soma das observações no iº tratamento
e as médias do iº tratamento são
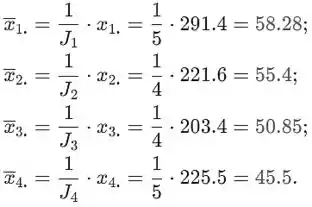
Passo 2
então a probabilidade de
é aproximadamente para todo e todo onde
O MSE foi calculado no exercício 22, e é
A quantidade pode ser encontrada no apêndice, e neste caso é
O objetivo é calcular os intervalos de confiança para cada onde , e observe se zero pertence aos intervalos. Se isso acontecer, o μ não são significativamente diferentes.
Calcular primeiro necessário para os intervalos de confiança como
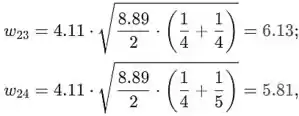
E o último
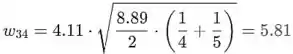
As diferenças correspondentes (respectivamente para dados acima) são
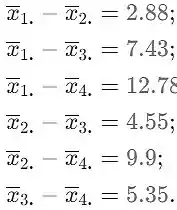
Passo 3
Os intervalos de confiança
pode ser calculado agora usando
onde tudo foi calculado; assim, os intervalos são, respectivamente, para as diferenças dadas acima
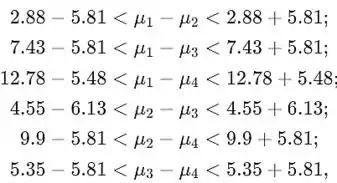
ou igualmente
Os intervalos de confiança das seguintes diferenças incluem zero
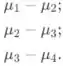
Assim, conclui-se que não há diferenças significativas entre as médias verdadeiras dos tratamentos 1 e 2; 2 e 3; 3 e 4. No entanto, há diferença significativa nas médias verdadeiras de outras combinações.
Resposta
Não há diferenças significativas entre as médias verdadeiras dos tratamentos 1 e 2; 2 e 3; 3 e 4.