Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 22
Aplique o teste de Wilcoxon para os dados do Exemplo 13.10.
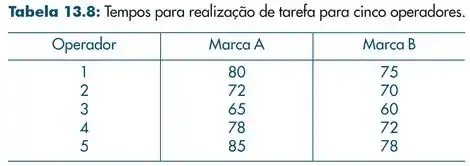
Exemplo 13.10: Cinco operadores de certo tipo de máquina são treinados em máqui-
nas de duas marcas diferentes, A e B. Mediu-se o tempo que cada um deles gasta na
realização de uma mesma tarefa, e os resultados estão na Tabela 13.8.
Passo 1
Lembrando que como os resultados são recolhidos analisando um mesmo operador em duas situações, trata-se de um problema com populações Pareadas.
Sendo nossa variável:
Queremos realizar o seguinte Teste de Hipótese:
Passo 2
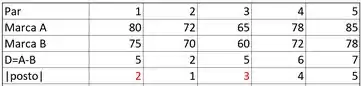
- Primeiramente devemos tomar a diferença dos pares:
- Agora, vamos atribuir valores numéricos em ordem crescente para as diferenças obtidas:
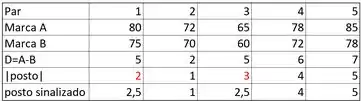
- Como tivemos um empate, devemos tirar a mediana dos postos onde houve repetição do valor encontrado para a diferença
- Agora, vamos atribuir aos postos o sinal devido a diferença:
- Dessa forma podemos encontrar a estatística , ela pode ser a soma dos postos negativos ou a soma dos postos positivos, de forma geral, sempre optamos pela soma de menor valor.
E
Passo 3
Ou seja, devemos optar pela estatística .
Vamos buscar na tabela da estatística de Wilcoxon, o valor crítico de forma que se então devemos rejeitar a hipótese nula (tomando
Da tabela, encontramos que,
Resposta
Portanto, como , devemos rejeitar e concluímos que demora-se mais para realizar uma tarefa com a máquina A.