Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 17b
Pacientes resolveram processar a clínica de emagrecimento Linha Fina sob a alegação de que o tratamento empregado não contribui para a diminuição do peso. O advogado de defesa contratou um estatístico que selecionou, aleatoriamente, 10 prontuários que continham informação a respeito dos pesos dos pacientes, tomados no início e no final do tratamento. Os dados obtidos foram (em kg):
- Faça uma análise descritiva para os dados e obtenha uma conclusão preliminar.
- Verifique se a conclusão do item anterior tem suporte estatístico. Formule as hipóteses adequadas e encontre a região crítica correspondente a
Passo 1
Na letra A vimos uma potencial redução nos pesos dos pacientes após o tratamento; agora precisamos confirmar isso utilizando testes de hipóteses.
Lembrando que estamos estudando a seguinte variável:
Como as medições são feitas antes e depois em um mesmo paciente, temos amostras pareadas, o que significa que devemos usar a seguinte aproximação:
Onde é a média das DIFERENÇAS, ou seja precisaremos tirar a diferença entre os pesos antes e depois em cada paciente; vamos adotar o seguinte então:
Com isso obteremos as seguinte diferenças:
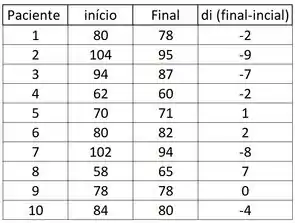
Passo 2
Com isso, podemos obter a média da diferença lembrando que não devemos ignorar os sinais, muito cuidado com isso:
E a variância:
Antes de mais nada agora, vamos definir nossas hipóteses:
Note o seguinte, temos que responder se o tratamento é efetivo ou não, como fizemos , para que o tratamento tenha surtido efeito o peso final tem de ser menor do que o inicial, por isso estamos testando se essa diferença é realmente menor do que zero ou não.
Ta comigo??! Seguimos!
Passo 3
Vamos agora definir nossa região crítica utilizando
Ou seja, precisamos de um valor tal que:
Mas, na tabela de t-student não temos valores de , temos somente de . Mas quem raios é isso?
Então, o é definido conforme a nossa região crítica; como a nossa é UNILATERAL então ele será dado por:
Portanto, deveremos ir na coluna de , muita atenção nisso!
E iremos na linha de graus de liberdade:
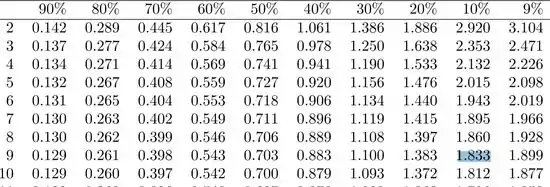
Portanto, nossa RC será dada por:
Finalmente podemos realizar o teste sob , lembrando que fazemos sob a hipótese nula porque ela apresenta o sinal de igual, e então podemos substituir na aproximação:
Olha só, NÃO pertence à região crítica, portanto devemos ACEITAR a hipótese nula.
Resposta
Ou seja, as evidências não apontam para uma redução efetiva dos pesos dos pacientes; portanto não podemos afirmar que o tratamento realmente funciona.