Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 21
Quatro diferentes espécies de milho foram produzidas em laboratório. Deseja-se testar, a um nível de significância de , se existe diferença estatisticamente significativa entre as produtividades. Para tanto, foram montados 34 canteiros, plantando-se neles o mesmo número de sementes e garantindo-se a todos as mesmas condições de fertilidade, irrigação e exposição à luz solar. Após um período de tempo pré-especificado, a produção de cada canteiro, em kg, foi obtida. Os resultados observados sofreram um tratamento inicial, e as seguintes informações foram disponibilizadas:
O que pode ser concluído com base na tabela?
Passo 1
Bom, você já deve estar ciente do quanto essa parte da matéria é longa e chata, acho que nem deveríamos chamar de Análise de Variância (ANOVA), mas sim de Velozes e furiosos.
Antes de mais nada vamos definir quem é a variável em questão:
Feito isso, vamos definir agora quem são as nossas hipóteses de teste:
Peraí, o que quer dizer “pelo menos um par”? Temos 4 amostras certo? Então na hipótese alternativa estamos dizendo que PELO MENOS duas dessas amostras se comportam de maneira diferente.
Ou seja, podemos ter , como podemos ter . Esse teste serve só para dizer se as 4 populações são iguais ou não, ele não consegue identificar onde esta o sinal de .
Agora, para realizar o teste precisamos utilizar a seguinte aproximação:
Chamamos isso de Distribuição com graus de liberdade.
Vamos destrinchar essa fórmula, é o numero de populações de quem tiramos as amostras, no caso temos . Enquanto que é o tamanho total das amostras, ou seja é a soma de todos os dados na tabela no enunciado.
Uma tabela ANOVA temo seguinte formato:
Vamos atrás de cada um desses dados.
Passo 2
Como sua calculadora passou a noite?? Espero que esteja de bem com ela!
Esses são os dados cruciais, note ainda que:
Facilita um pouco.
Agora, a grande questão é que precisamos obter alguns dados para poder jogar nessas fómulas aí de ; com muito foco força e fé, vamos a eles:
Vamos começar com a média GERAL; note o seguinte:
Então, isolando:
A média GERAL é dada pela soma de todos os dados, de todas as amostras, divido pelo tamanho total:
Capitou a ideia? Então:
Beleza, agora outra coisa que precisamos para jogar naquelas fomulas, é o seguinte:
Para encontrar isso, vamos ter que usar a variância dada na tabela do enunciado, da um olhada:
Então podemos isolar:
E após fazer isso para todos as 4 amostras, podemos somar tudo e obter:
Sim! É espantoso, eu sei. Mas carmeia que no final da tudo certo!!
Ainda antes de jogar tudo naquelas fórmulas la, precisamos de um último dado:
Esse é bem mais trivial, basta multiplicar o tamanha de cada amostra pela sua respectiva média:
Cá entre nós, estar assistindo um velozes agora ia ser muito top...
Passo 3
Então, basta tacar tudo naquelas fórmulinhas da tabela lá:
E
Ufa, agora estamos quase...Prometo.
Agora, para montarmos a tabela ANOVA, é importanto que você saiba como calculamos os “quadrados médios”, pois usamos eles para realizar o teste lembra??
E
Finalmente nossa Tabela ANOVA:
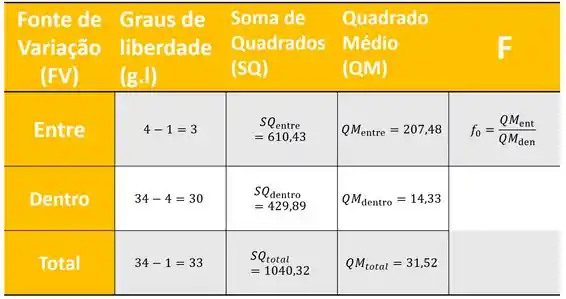
Agora, antes de realizar o teste , precisamos da nossa região crítica adotando :
Precisaremos ir na tabela de distribuição de buscar um tal que:
Portanto, deveremos ir na tabela que representa , ir na coluna de graus de liberdade, e na linha de graus de liberdade:
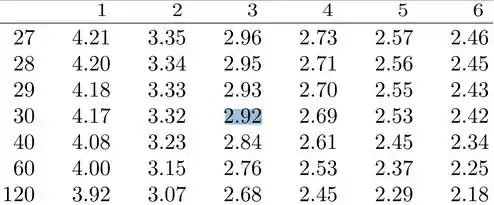
Portanto nossa RC:
E finalmente, o nosso teste:
Portanto, como PERTENCE a região crítica, vamos REJEITAR a hipótese nula.
Foi impressão minha, ou realmente dava tempo de assistir os 15 filmes do velozes e furiosos antes de terminar essa questão??
Resposta
Concluimos que a produtividade em cada canteiro não são todas iguais, evidenciando uma diferença entre as espécies plantadas.