Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 61
Um artigo no Journal of materials engineering (1989, Vol 11) reportou os resultados de um experimento para determinar os mecanismos de falha em revestimentos em barreiras térmicas com plasma vaporizado. A tensão de falha, para um revestimento particular sob duas condições diferentes de teste, é dada a seguir:
Tensão de falha depois de 9 ciclos de 1 hora: .
Tensão de falha depois de 6 ciclos de 1 hora:
(a)Quais as suposições necessárias para construir intervalos de confiança para a diferença na tensão média de falha, sob as duas condições diferentes de teste? Use os gráficos de probabilidade normal dos dados para verificar essas suposições?
(b)Encontre um intervalo de confiança 99% para a diferença na tensão média de falha, sob as duas condições diferentes de teste.
(c)Usando o intervalo de confiança construído no item (b), a evidência confirma a afirmação de que as primeiras condições de teste fornecem resultados melhores, em média, do que as segundas condições? Explique sua resposta.
(d)Construa um intervalo de confiança de 95% para a razão de variâncias da tensão de falha sob as duas condições diferentes de teste.
(e)Use sua resposta no item (b) para determinar se há uma diferença dignificativa nas varianças da duas condições diferentes de teste. Explique sua resposta.
Passo 1
Opa, tranquilo galera? Espero que sim! Se não, bora resolver essa questão de estatística e ficar suave! Então, para o item a) temos que: para essa suposição de uma média de tempo calculada por:
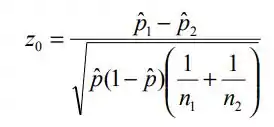
No item b) a gente pode encontrar esse intervalo a partir da formula onde
Passo 2
c) Não, pela falta de dados.
d)
e)Não há para calcular.
Resposta
a)
b)Não
c)
d)
e)