Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 46

Sejam X e Y a concentração e a viscosidade de um produto químico. Suponha que XY tem uma distribuição normal be variada, com desenho, aproximadamente, uma curva de nível das funções densidade de probabilidade conjunta para cada um dos seguintes valores de P.

Passo 1

Para a Distribuição Normal Bivariada (X, Y), os parâmetros que temos são desvio padrão, média e correlação. Pode ser escrito como:

Usando essas duas matrizes acima, você pode desenhar um gráfico de contorno nos programas (usei Python).

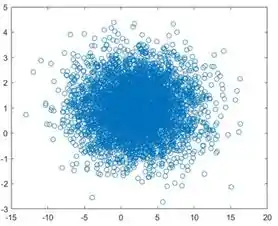
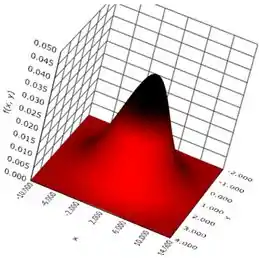
Pelas fotos você pode notar que as variáveis não estão correlacionadas.

Passo 2

Na letra b:

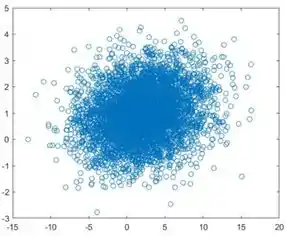
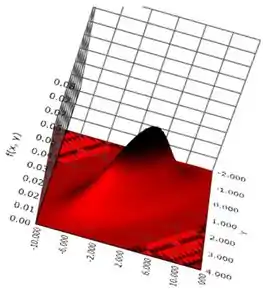
A partir dessas duas imagens, você pode ver que as variáveis são altamente correlacionadas positivamente.

Passo 3

Letra c:

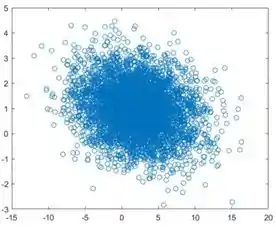
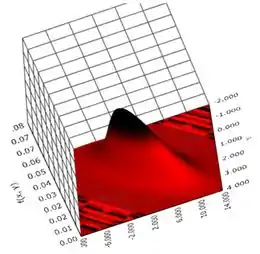
Você pode notar que as variáveis estão correlacionadas, mas na direção oposta (correlação negativa).

Resposta

Ver gráficos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que X e Y sejam variáveis aleatórias independentes com densidades de probabilidade g x = 8 x 3 , x2 0 ,c a s oc o n t r á r i o á E h y = 2 y , 0y1 0 ,c a s oc o n t r á r i o á Determine o va

Sejam X o número que ocorre quando um dado vermelho é jogado e Y , o número que ocorre quando um dado verde é jogado. Determine(a) E ( X + Y ) ;(b) E ( X - Y ) ;(c) E ( X Y ) .

Suponha que você jogue um dado, não adulterado, de dez lados (0, 1, 2, ..., 9) 500 vezes. Usando o teorema de Chebyshev, calcule a probabilidade de que a média amostral, X , esteja entre 4 e 5.

Prove o teorema de Chebyshev quando X for umavariável aleatória discreta.

Considere o Exercício 4.10. Pode-se dizer que as notas dadas pelos dois especialistas são independentes? Explique.