Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 7.Exercícios - Ex. 33
artigo "Measuring and Understanding the Aging of Kraft Insulating Paper in Power Transformers" (IEEE Electrical Insul. Mag.. 1996, p. 28-34) continha as seguintes observaçoes sobre o grau de polimerizaçăo dos espécimes de papel para os quais a viscosidade vezes a concentração caíram em certo intervalo intermediário:
a. Construa um boxplot dos dados e comente quaisquer características interessantes.
b. É plausível que as observações da amostra fornecidas tenham sido selecionadas de uma distribuição normal?
c. Calcule o intervalo de confiança de bicaudal para o grau médio real de polimerização (como fizeram os autores do artigo). intervalo sugere que 440 seja um valor plausivel para o grau médio real de polimerizaçaro? E quanto a 450 ?
Passo 1
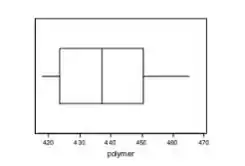
a. O boxplot indica um desvio positivo muito leve, sem outliers. Os dados parecem centrar-se perto de 438 .
Passo 2
b. Com base em um gráfico de probabilidade normal, é razoável supor que as observações da amostra vieram de uma distribuição normal.
Passo 3
c. Com d.f. , o valor crítico para C.I. is e o intervalo é
Como 440 está dentro do intervalo, 440 é um valor plausível para a média verdadeira. 450 , no entanto, não é, pois está fora do intervalo.
Resposta
perto de 438
b. distribuição normal
c. 440