Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 54
Um artigo no periódico IEEE Transactions on Componentes, Hybrids and Manufacturing Technology (1992, Vol.15) descreve um experiment para investigar um método de alinhamento de chips ópticos em placas de circuitos. O método envolve colocar pingos de solda e três métodos de alinhamento. A variável de resposta é a exatidão do alinhamento (em micrômetros). Os dados são:
Há qualquer indicação de que tanto o tamanho dos pingos de solda como o método de alinhamento afetem a exatidão do alinhamento? Há qualquer evidência de interação entre esses fatores? Use .
Que recomendações você faria a respeito desse processo?
Analise os resíduos desse experimento. Comente a adequação do modelo.
Passo 1
Bom galera, considerando a tabela o modelo estatístico linear do experimento é:
As hipóteses que teremos que testar são:
(Não tem efeito do tamanho do pingo de solda)
Pelo menos um
(Não tem efeito do método de alinhamento)
Pelo menos um
(Não tem interação)
Pelo menos um
Passo 2
Beleza, agora usando o Minitab para fazer a análise de variância. Nós encontraremos:
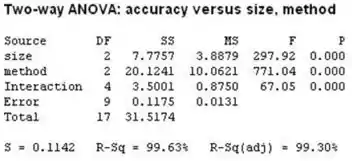
Então, temos que o valor de para o tamanho dos pingos de solda é menor do que . Portanto, rejeitamos a hipótese nula, logo vemos que o tamanho dos pingos de solda afetam a precisão do alinhamento.
Já o valor de para o método de alinhamento é menor que . Então, podemos rejeitar a hipótese nula e concluímos que o método de alinhamento afeta a precisão do alinhamento.
Por último o valor de para o valor da interação é menor que . Portanto, rejeitamos a hipótese nula e concluímos que há interação entre o tamanho do pingo de solda e o método de alinhamento.
Passo 3
Show de bola, ainda no Minitab, podemos gerar um gráfico da interação:
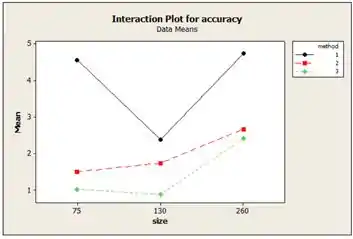
Com esse gráfico, podemos ver que há uma interação entre o tamanho do pingo de solda e o método de alinhamento, uma vez que todas as três linhas não são paralelas. A eficácia do alinhamento do chip aumenta quanto maior for o valor. Logo, o método de alinhamento com precisão de solda de diâmentros é o mais eficaz.
Nesse caso, a interação é significativa. Então poderíamos aplicar um procedimento como o método LSD de Fisher aos meios de fator “tamanho”, com fator “método” definido em um determinado nível.
Passo 4
Por fim, ainda no Minitab, geramos os gráficos dos resíduos:
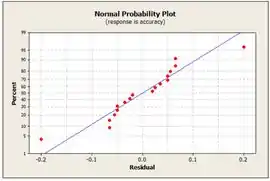
No gráfico, temos a parcela de probabilidade normal de resíduos. Esse gráfico tem uma linha reta passando pelo centro do gráfico indicando que os resíduos tem uma distribuição normal.
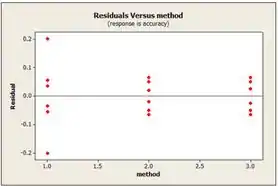
Já no e gráfico representam a parcela de resíduos versus do tamanho e do método, respectivamente. Com o gráfico, o tamanho da colisão da solda de de diâmetro tem a maior variabilidade no alinhamento do chip óptico do que os outros tamanhos. E com o gráfico vemos que o método de alinhamento tem a maior variabilidade no alinhamento dos chip.
E no gráfico de resíduos versus valor ajustado mostra que temos resíduos mais elevados à medida que o valor resposta aumenta. Isso sugere que é preciso haver alguma transformação da variável resposta.
Resposta
O tamanho dos pingos e o método de alinhamento afetam a precisão do alinhamento, e existe interação entre o tamanho dos pingos e o método de alinhamento.
O método de alinhamento com precisão de solda de diâmentros é o mais eficaz.