Um artigo no periódico Journal of Manufacturing Systems (Vol. 10, 1991, pp. 32-40) descreve um experiment para investigar o efeito de quatro fatores pressão do jato de água. velocidade transversal do jato sobre a rugosidade de uma superfície de um cortador com jato de água. Um planejamento é mostrado a seguir.
Estime os efeitos dos fatores.
Tente um modelo pelo exame de um gráfico de probabilidade normal dos efeitos.
O modelo do item é uma descrição razoável do processo?
A falta de ajuste é significativa? Use
Interprete os resultados desse experimento.
Analise os resíduos desse experimento.
Passo 1
Bom galera, vamos considerar o design fatorial , então ficamos com:

Passo 2
Belezinha, agora vamos estimar os efeitos dos fatores, usando o Minitab, encontraremos:
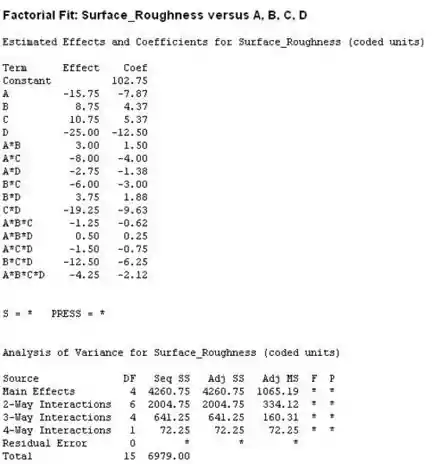
Passo 3
Agora, usando denovo o Minitab nós podemos plotar o gráfico de probabilidade normal dos efeitos, temos então:

A partir do gráfico, podemos inferir que o efeito de é um fator significativo, uma vez que esses pontos passam um pouco distante dos outros pontos. Portanto, o modelo de tentativa a partir do gráfico é:
Passo 4
Então, fazemos a analise de variância no Minitab, o resultado é:
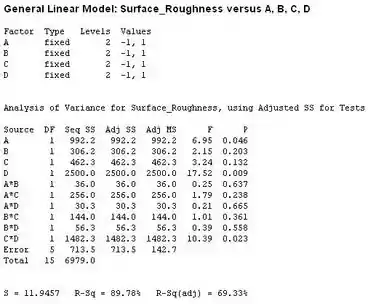
A partir da tabela de analise de variância, a gente pega o valor para os fatores , e a interação , e descobre que são menores que o . Portanto, os fatores , e a interação são significantes. Logo, em parte há uma falta de ajuste significativo.
Passo 5
O modelo que a gente usa para descrever o processo é:
Onde a interceptação é a média geral das observações e é a metade do valor estimado de , é o efeito estimado para e é o efeito estimado para .
Passo 6
Por fim, vamos motar uma tabela dos valores estimados e os resíduos do nosso modelo:

Plotando o gráfico de normalidade dos resíduos ficamos com:

E vemos que os resíduos estão aproximadamente ao longo de um linha reta. Portanto, não há nenhum problema com a normalidade nos dados.
Resposta
; ; ; ; ; ; ; ; ; ; ; ; ; ;
Os fatores , e são significantes.
A interceptação é a média geral das observações e é a metade do valor estimado de , é o efeito estimado para e é o efeito estimado para .
Os resíduos estão aproximadamente ao longo de um linha reta. Portanto, não há nenhum problema com a normalidade nos dados.