Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 75
O artigo “Photocharge Effects in Dye Sensitized Ag(Br,I] Emulsions at Millisecond Range Exposures” (Photographic Sci. and Engr., 1981, p. 138–144) apresenta os dados a seguir sobre x % de absorção de luz em 5800 A e y = fotovoltagem de pico.
a. Construa um gráfico de dispersão desses dados. O que ele sugere? b. Supondo que o modelo de regressão linear simples seja apropriado, obtenha a equação da reta de regressão estimada. c. Que proporção da variação observada na fotovoltagem de pico pode ser explicada pela relação do modelo? d. Preveja a fotovoltagem de pico quando a % de absorção for 19,1 e calcule o valor do resíduo correspondente. e. Os autores desse artigo afirmam que existe uma relação linear útil entre a % de absorção e a fotovoltagem de pico. Você concorda? Realize um teste formal. f. Apresente uma estimativa da mudança na fotovoltagem de pico esperada, associada com um aumento de 1% na absorção de luz. Sua estimativa deve transmitir informações sobre a precisão da estimação. g. Repita o item (f) para o valor esperado de fotovoltagem de pico quando a % de absorção for 20.
Passo 1
- A estimativa de mínimos quadrados da inclinação é
- Agora x é a taxa de passada enquanto y representa a velocidade.
- O coeficiente de determinação, , é
A estimativa de mínimos quadrados da interceptação é
Usando os valores dados no exercício, a estimativa de é
O modelo de regressão linear simples para prever a taxa de passada a partir da velocidade é
Passo 2
Usando os valores fornecidos no exercício, a estimativa de é
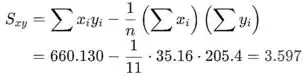
E o valor de
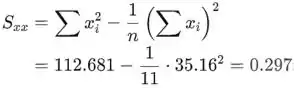
assim, a estimativa da inclinação é
A estimativa do intercepto é
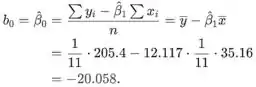
O modelo de regressão linear simples para prever a velocidade a partir da taxa de passada é
Passo 3
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
A soma total dos quadrados é
No entanto, o coeficiente de determinação pode ser calculado usando a fórmula
Os dados não são fornecidos; assim, esta é a única maneira de calcular o coeficiente de determinação.
No caso de (a), o coeficiente de determinação é
no caso de (b) (b), o coeficiente de determinação é
Isso é esperado. Se você não obtiver o mesmo valor para o coeficiente de determinação, talvez seja por causa do arredondamento - eles devem ser exatamente os mesmos!