Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 68

O artigo “Refuse–Derived Fuel Evaluation in an Industrial Spreader–Stoker Boiler” (J. Engr. for Gas Turbines and Power, 1984, p. 782–788) apresenta os dados a seguir sobre x % de entrada térmica de combustível derivado rejeitado (RDF) e y % eficiência de uma determinada caldeira

a. Obtenha a equação da reta de regressão estimada. b. O modelo de regressão linear simples especifica uma relação útil entre a % de entrada térmica de RDF e a % de eficiência? Expresse e teste as hipóteses apropriadas. c. Para obter uma estimativa precisa de1, teria sido preferível fazer quatro observações em x 0 e quatro observações em x 50 (supondo que o modelo seja válido para x entre 0 e 50)? E no caso de três observações em x 0 e três em x 50? Explique. d. Estime a % média real de eficiência quando a % de entrada térmica de RDF é 25, usando um IC de 95%. A % média real de eficiência parece ter sido estimada de maneira precisa? Explique.

Passo 1

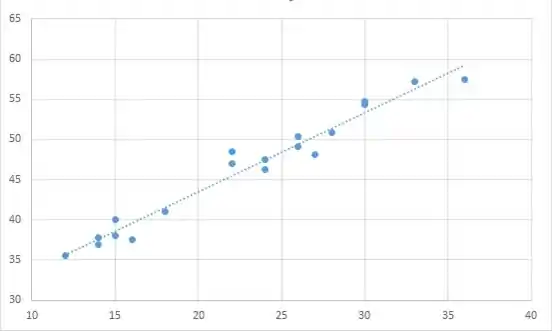
  1. O preço de venda não é determinado exclusivamente pela altura. Por exemplo, quando a altura é 22, o preço de venda é 48,5 ou 47, o que significa que não é determinado exclusivamente.
  2. O gráfico de dispersão sugere que o modelo de regressão linear simples pode ser utilizado.

    3. Passo 2

  3. A estimativa de mínimos quadrados da inclinação na linha de regressão   y = β 0 + β 1 x + ϵ

    4. b 1 = β ^ 1 = ∑ x i - x ¯ ( y i - y ¯ ) ∑ ( x i - x ¯ ) ² = S x y S x x

    S X y = ∑ x i y i - 1 n ∑ x i ∑ y i

    S x x = ∑ x i 2 - 1 n ∑ x i 2

    A estimativa de mínimos quadrados do intercepto é

    b 0   = β ^ 0 = ∑ y i - β ^ 1 ∑ x i n = y ¯ - β ^ 1 x ¯

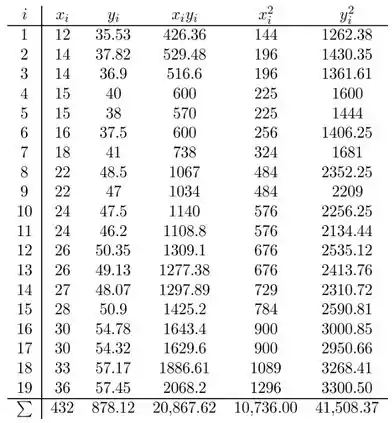
    As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados

    ∑ x i y i = 12 ∙ 35.53 + 14 ∙ 37.82 + … + 36 ∙ 57.45 = 20867.62

    ∑ x i = 12 + 14 + … + 36 = 432 ;

    ∑ y i = 35.53 + 37.82 + … + 57.45 = 878.12 ;

    ∑ x i 2 = 12 2 + 14 2 + … + 36 2 = 10736.00 ;

    ∑ y i 2 = 35.53 2 + 37.82 2 + … + 57.45 2 = 41508.37

    S x y = ∑ x i y i - 1 n ∑ x i ∑ y i

    = 20867.62 - 1 19 ∙ 432 ∙ 878.12

    = 901.94

    S x x = ∑ x i 2 - 1 n ∑ x i 2

    = 10736.00 - 1 19 432 2

    = 913.68

    β ^ 1 = S x y S x x = 901.94 913.68 = 0.987150922

    Encontrando y ¯   e   x ¯ usando as somas dadas no exercício, a estimativa do intercepto é

    β ^ 0 = y ¯ - β ^ 1 x ¯

    = 1 19 878.12 - 0.987 19 432

    = 23.77215

    y ^ = 23.772 + 0.987 x

  4. O valor ajustado   y 1 ^ , y 2 ^ , … , y n ^ são valores obtidos substituindo x 1 , x 2 , … , x n na linha de regressão. Os residuais são a diferença entre os valores observados e ajustados.

    5. A estimativa pontual quando x=27 é

    y ^ = 23.772 + 0.987 ∙ 27 = 50.425

    Assim, o resíduo é

    ϵ 1 = 48.07 - 50.425 = - 2.355

  5. O valor requerido é o coeficiente de determinação. O coeficiente de determinação, r 2 , é

r 2 = 1 - S S E S S T

A soma dos quadrados dos erros, SSE, é

S S E = ∑ y i - y i ^ 2 = ∑ [ y i - ( β ^ 0 + β ^ 1 x i )   ] ²  

A fórmula computacional para SSE é

S S E = ∑ y i 2 - β ^ 0 ∑ y i - β ^ 1 ∑ x i y i = S y y - β ^ 1 S x y

A soma total dos quadrados é

S S T =   S y y = ∑ y i - y ¯ 2 = ∑ y i 2 - 1 n ∑ y i 2

S T T = S y y = ∑ y i 2 - 1 n ∑ y i 2

= 41508.37 - 1 19 ∙ 878.12 2

= 924.44

S S E = ∑ y i 2 - β ^ 0 ∑ y i - β ^ 1 ∑ x i y i

= 41508.37 - 23.772 ∙ 878.12 - 0.987 ∙ 20867.62

= 34.08

r 2 = 1 - S S E S S T = 1 - 34.08 924.44 = 0.963

ou igualmente 96.3% da variação observada atribuída à relação linear aproximada.

Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

12-70. Considere os dados de concentracão de arsenio do Exereicio 12-10.a) Discuta como vocé modelaria a informação sobre o sexo da pessoa.b) Ajuste um modelo de regressão para o arsénio nas unhas. us
12-76. Considere os dados de resisténcia à tração de um fio do Exerci-cio 12-6. Construa modelos de regressão para os dados, usando os se-guintes métodos:a) Todas as regressoes possíveis. Encontre as
12-75.Considere o ajuste de um moxlelo de regressão aos dadus de umamistura de carvão e calcário do Exercicio 12-11.Use densidade como aresposta. Construa modelos de regressão para os dados, usando as
12-72.Considere os dados de acabamento de superficie de Exemplo 12.13. Teste a hipótese de que dois modelos diterentes de regressao(comdiferentes inclinaçues e interseções) sào requeridos para modelar
12-74.Considere os dados de energia eletrica do Exercicio 12-4. Cons-trua modelos de regressão para os dados, usando as seguintes técnicas:a) Todas as regressie's possiveis. Encontre as equaçoes que m