Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 51
Um artigo em Process Engineering (1992, Nº 71, pp. 46-47) apresenta um experimento fatorial, Com dois fatores, usado para investigar o efeito do e da concentração de catalisador sobre a viscosidade () do produto. Os dados são:
Teste os efeitos principais e interações usando . Quais são as suas conclusões?
Faça um gráfico da interação e discuta a informação fornecida por esse gráfico.
Analise os resíduos desse experimento.
Passo 1
Bom galera, considerando a tabela o modelo estatístico linear do experimento é:
As hipóteses que teremos que testar são:
(Não tem efeito no pH)
Pelo menos um
(Não tem efeito da concentração do catalisador)
Pelo menos um
(Não tem interação)
Pelo menos um
Passo 2
Beleza, agora usando o Minitab para fazer a análise de variância. Nós encontraremos:
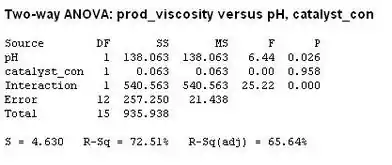
Então, temos que o valor de para o pH é menor do que . Portanto, rejeitamos a hipótese nula, logo vemos que o pH afeta a viscosidade do produto.
Já o valor de para a concentração do catalisador é maior que . Então, não podemos rejeitar a hipótese nula e concluímos que a concentração do catalisador não afeta a viscosidade do produto.
Por último o valor de para o valor da interação é menor que . Portanto, rejeitamos a hipótese nula e concluímos que há interação entra pH e concentração do catalisador.
Passo 3
Show de bola, ainda no Minitab, podemos gerar um gráfico da interação:
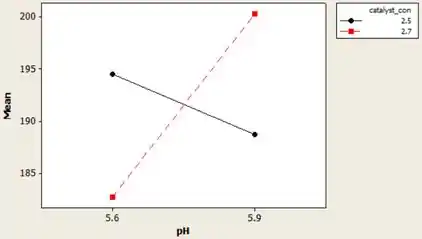
Com esse gráfico, podemos ver que há uma interação entre o pH e concentração de catalisador, uma vez que duas linhas estão conectadar uma à outra. A maior valor é mais efetiva na viscosidade do produto. Portanto, o nivél de de pH com concentração de catalisador de é mais eficaz.
Passo 4
Por fim, ainda no Minitab, geramos os gráficos dos resíduos:
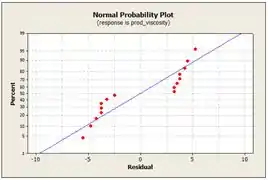
No gráfico, temos a parcela de probabilidade normal de resíduos. Esse gráfico tem pontos que caem um pouquinho fora da linha reta, isso indica que há alguns problemas com a suposição de normalidade.
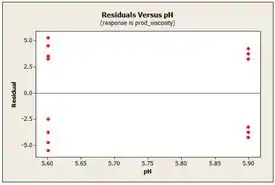
Já no e gráfico representam a parcela de resíduos versus pH e concentração do catalisador, respectivamente. O nível de pH tem maior variabilidade na viscosidade do produto do que o nível de pH . Os níveis de concentração do catalisador fornecem uma variabilidade parecida na viscosidade do produto.
E no gráfico de resíduos versus valor ajustado não temos nenhum padrão incomum.
Resposta
A viscosidade do produto é afetada pelo pH e não pela concentração do catalisador, mas a há interação entre o pH e a concentração do catalisador.
O nivél mais eficaz de de pH com concentração de catalisador de .