artigo "The Undrained Strength of Some Thawed Permafrost Soils" (Canadian Geotechnical J., 1979, p. 420-427) contém os dados a seguir sobre a resistência ao corte sem drenagem de solos arenosos ( , em kPa), profundidade volume de água

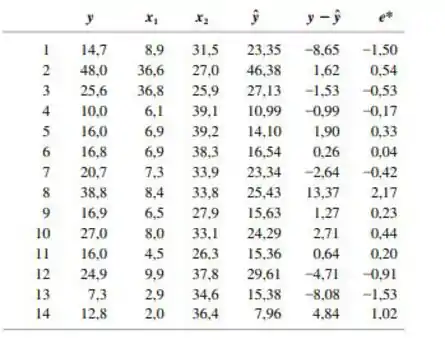
Para calcular os valores previstos e os resíduos, foi ajustado um modelo quadrático completo, que gerou a função de regressão estimada

a. Os gráficos de versus versus e e* versus sugerem que o modelo quadrático completo deve ser modificado? Justifique sua resposta.

b. O valor de para o modelo quadrático completo é 0,759. Teste as hipóteses nulas no nível 0,05 estabelecendo que não há nenhuma relação linear entre a variável dependente e qualquer um dos cinco previsores.

c. É possível mostrar que . A estimativa de é base no modelo quadrático completo). Primeiro obtenha o desvio padrão estimado de e, em seguida, estime o desvio padrão de (isto é, ) quando e ) quando e 33,1 Por fim, calcule um IC de para a resistência média. [Sugestāo: Qual é ?]

d. Se calibrarmos o modelo de primeira ordem com a função de regressão , obteremos . Usando o nível 0,05 , teste a hipótese nula que expressa que todos os termos quadráticos podem ser excluídos do modelo.

O valor de para o modelo quadrático completo é 0,759. Teste as hipóteses nulas no nível 0,05 estabelecendo que não há nenhuma relação linear entre a variável dependente e qualquer um dos cinco previsores

b. , so será rejeitado se , então rejeitamos . Pelo menos um dos coeficientes não é igual a zero.

É possível mostrar que . A estimativa de é base no modelo quadrático completo). Primeiro obtenha o desvio padrão estimado de e, em seguida, estime o desvio padrão de (isto é, ) quando e ) quando e 33,1 Por fim, calcule um IC de para a resistência média.

c. Quando e a residual é e o padrão residual é ; uma vez que do residual), sd do residual. Então a variância estipulada é , então o estimado sd é 3.304. Uma vez que e , o desejado C.I.é

, so será rejeitado se . Com , e , e uma vez que não é não pode ser rejeitado e todos os termos quadráticos devem ser excluídos. (n.b.: esta não é uma modificação que seria sugerida por uma parcela residual.