Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 13.Exercícios - Ex. 23
a)Use o método MDS de Fisher, para o experimento no material supercondutor descrito no exercício 13-8. Que métodos de preparação diferem, se ?
b)Use o método gráfico para comparar as médias descritas nessa seção e compare suas conclusões com aquelas do método MDS de Fisher.
Passo 1
Hey, jovem, tudo bem contigo? Espero que sim 😊 Bora pra mais uma questãozinha de estatística? O assunto dessa questão trata sobre MDS de Fisher, e vamos focar nele como um método pra comparar com médias através de métodos gráficos, afinal, vamo ver qual se aplica melhor na nossa conclusão.
Passo 2
Para o item a), ele pergunta pra gente que métodos de preparação diferem para o coeficiente de controle . Para MDS de Fisher, e o método de médias móveis variáveis (MMV) se diferem por causa da quantidade baixa de amostras, no qual a MDS de Fisher se assemelha mais ao método gráfico, dando mais clareza!
Passo 3
Para o gráfico desse item, a gente tem:
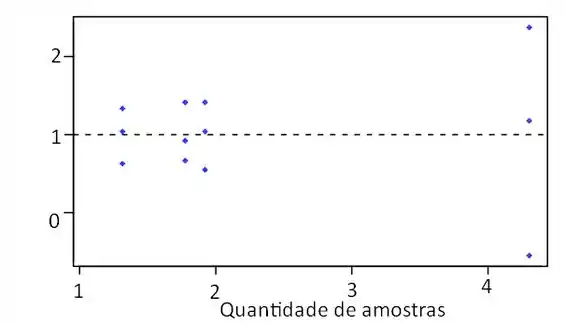
Sendo a linha pontilhada a média para o exercicio, podemos ver que assim como o método de Fisher, para menores amostas e maiores amostras, a média permanece constante. Sendo assim, Fisher e o método gráfico são bem semelhantes, como esperado!