Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 88
Automóveis chegam em uma estação de inspeção de equipamentos veiculares de acordo com um processo de Poisson com taxa 10 por hora. Suponha que, com probabilidade 0,5, um veículo chegue sem violações de equipamento. a. Qual é a probabilidade de exatamente 10 veículos chegarem durante uma hora e nenhum ter violações? b. Para qualquer y 10 fixo, qual é a probabilidade de y veículos chegarem em uma hora, todos sem violações? c. Qual é a probabilidade de 10 carros sem violações chegarem na próxima hora? [Sugestão: Some as probabilidades na parte (b) entre y 10 e .]
Passo 1
- P(X = 10 e sem violações) = P(sem violações | X = 10) × P(X = 10)
- P(y chegam e exatamente 10 não têm violações) = P(exatamente 10 não tem violações | y chega)
- P (exatamente 10 sem violação) =
Passo 2
Passo 3
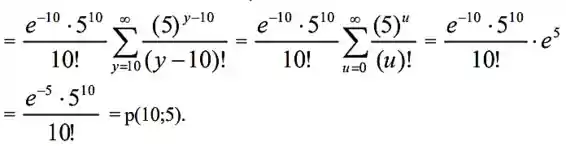
De fato, generalizar esse argumento mostra que o número de chegadas “sem violação”
dentro da hora tem uma distribuição de Poisson com parâmetro 5; os 5 resultados de p = 10(.5).
Resposta
Ver o desenvolvimento