Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 2
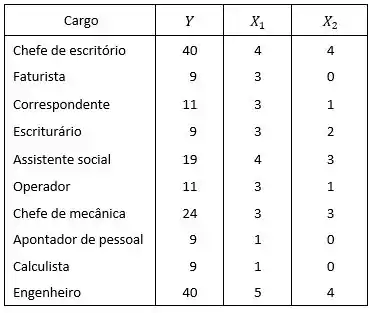
Em uma avaliação de cargos, pelo método dos pontos, o salário (), expresso em Cr$ 100,00, está relacionado com o nível de instrução () e com o nível de supervisão () pela fórmula: . Estabelecer, pela análise de regressão, os valores de , e , e verificar quais os funcionários devem ter seus salários aumentados, a partir dos seguintes dados, obtidos numa empresa:
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo!
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para o caso de ter apenas duas variáveis explicativas:
Para encontrarmos os valores de , e , iremos utilizar as equações:
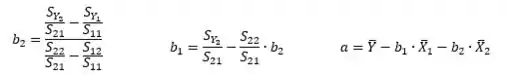
Onde iremos precisar calcular aas médias (, e ) pelas seguintes equações:
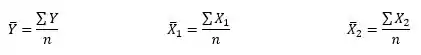
As variâncias vamos usar as equações:
E as covariâncias:
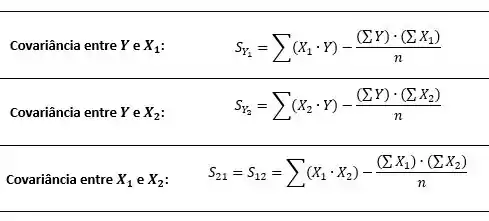
Passo 2
Então vamos lá para nosso exercício. Primeiramente iremos calcular os somatórios, para isso iremos utilizar a tabela descrita abaixo:
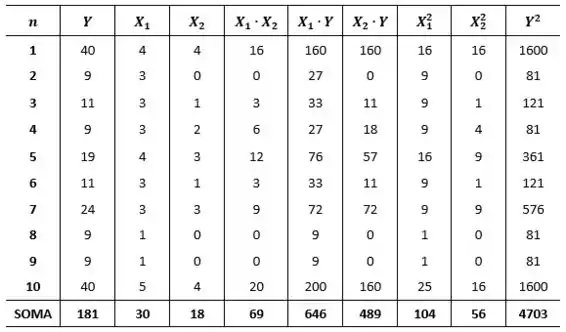
Agora vamos obter as médias de , e , respectivamente:
O cálculo das variâncias:
E das covariâncias:
Passo 3
Com esses valores, finalmente conseguimos calcular os valores de , e :
Por fim, temos a equação da regressão linear múltipla:
Utilizando a equação para comparar com os valores de , temos:
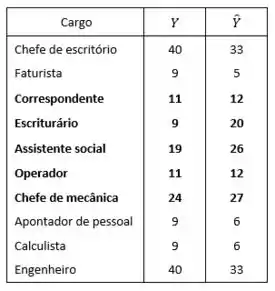
De acordo com equação da estimativa, os funcionários que devem ter aumento são: correspondente, escriturário, assistente social, operador e chefe de mecânica.
Tchau galera!
Resposta
. Aumento para correspondente, escriturário, assistente social, operador e chefe de mecânica.