Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.3 - Ex. 25

Caridade

A tabela seguinte mostra os resultados de uma pesquisa que perguntou a 2.850 pessoas se elas

estavam envolvidas em qualquer tipo de trabalho para caridade. Uma pessoa é selecionada aleatoriamente da amostra. Encontre a probabilidade de cada evento.

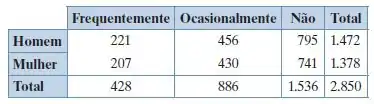
(a) A pessoa está frequente ou ocasionalmente envolvida com caridade.

(b) A pessoa é mulher ou não está envolvida com caridade.

(c) A pessoa é homem ou está frequentemente envolvida com caridade.

(d) A pessoa é mulher ou não está frequentemente envolvida com caridade.

Passo 1

Salve, fera! Tudo bem? Vamos encarar essa questão! Ela é bem simples.

(a) Analisando a tabela, temos que, a probabilidade da pessoa estar frequente ou ocasionalmente envolvida com caridade vai ser:

A = Probabilidade de estar frequentemente envolvida: P ( A ) = 428 2850 = 0 , 150

B = Probabilidade de estar ocasionalmente envolvida: P ( B ) = 886 2850 = 0 , 311

Probabilidade de A e B acontecer: P ( A   e   B ) = 0 pois são eventos mutuamente exclusivos.

Assim, a probabilidade de A ou B acontecer é dada por:

P A + P B - P A   e   B = 0 , 461

(b) Analisando a tabela, temos que, a probabilidade da pessoa ser mulher ou não estar envolvida com caridade vai ser:

A = Probabilidade de ser mulher: P ( A ) = 1 3 78 2850 = 0 , 483

B = Probabilidade de não estar envolvida: P ( B ) = 1536 2850 = 0 , 539

Probabilidade de A e B acontecer: P ( A   e   B ) = 741 2 8 50 = 0 , 260

Assim, a probabilidade de A ou B acontecer é dada por:

P A + P B - P A   e   B = 0 , 762

(c) Analisando a tabela, temos que, a probabilidade da pessoa ser homem ou estar frequentemente envolvida com caridade vai ser:

A = Probabilidade de ser homem: P ( A ) = 1 472 2850 = 0 , 516

B Probabilidade de estar frequentemente envolvida: P ( B ) = 428 2850 = 0,150

Probabilidade de A e B acontecer: P ( A   e   B ) = 22 1 2850 = 0,0 77

Assim, a probabilidade de A ou B acontecer é dada por:

P A + P B - P A   e   B = 0 , 589

(d) Analisando a tabela, temos que, a probabilidade da pessoa ser mulher ou não estar frequentemente envolvida com caridade vai ser:

A = Probabilidade de ser mulher: P ( A ) = 1378 2850 = 0,483

B = Probabilidade de não estar frequentemente envolvida: P B = 1 - 428 2850 = 0 , 8 50

Probabilidade de A e B acontecer: P ( A   e   B ) = 1171 2850 = 0 , 411

Assim, a probabilidade de A ou B acontecer é dada por:

P A + P B - P A   e   B = 0 , 922

Espero ter ajudado! Abraços e até a próxima!

Resposta

(a) 0,461

(b) 0,762

(c) 0,589

(d) 0,922

Exercícios de Livros Relacionados

O São Paulo Futebol Clube ganha com probabilidade 0,7 se chove e com 0,8 se não chove. Em Setembro a probabilidade de chuva é de 0,3 . O São Paulo ganhou uma partida em Setembro, qual a probabilidade
Considere um conjunto de 4 números dos quais nenhum deles é zero, dois são positivos e dois são negativos. Sorteamos ao acaso, com reposição, 2 números desse conjunto. Determine a probabilidade de:Um
Considere um conjunto de 4 números dos quais nenhum deles é zero, dois são positivos e dois são negativos. Sorteamos ao acaso, com reposição, 2 números desse conjunto. Determine a probabilidade de:c.
Uma moeda é viciada de modo que a probabilidade de sair cara é 4 vezes maior que a de sair coroa. Para 2 lançamentos independentes dessa moeda, determinar:c. A probabilidade de sair pelo menos uma car
Considere um conjunto de 4 números dos quais nenhum deles é zero, dois são positivos e dois são negativos. Sorteamos ao acaso, com reposição, 2 números desse conjunto. Determine a probabilidade de:O q