O São Paulo Futebol Clube ganha com probabilidade se chove e com se não chove. Em Setembro a probabilidade de chuva é de O São Paulo ganhou uma partida em Setembro, qual a probabilidade de ter chovido nesse dia?
Passo 1
Oi, tudo bem? Bora resolver esse exercício?
Queremos calcular a probabilidade de ter chovido no dia que o São Paulo ganhou uma partida no mês de Setembro.
Para facilitar o entendimento, vamos construir um diagrama de árvore:
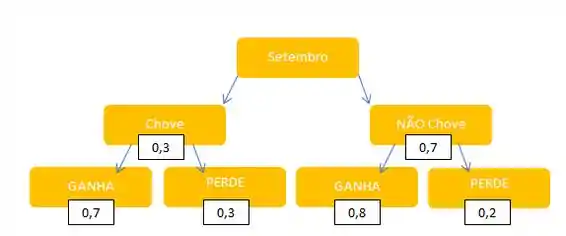
Passo 2
Queremos a probabilidade de ter chovido, dado que o São Paulo ganhou uma partida em Setembro. Certo?
Matematicamente,
Resposta
Assim, concluímos que