Enunciado

Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 2.Problemas - Ex. 13

Certa cidade com uma população de 100.000 habitantes possui 3 jornais: I, II e III. As proporções de moradores que leem esses jornais são as seguintes:

I: 10% / I e II: 8% / I e II e III: 1%

II:30% / I e III: 2%

III: 5% / II e III: 4%

(Essa lista nos diz, por exemplo, que 8.000 pessoas leem os jornais I e 11.)

(a) Determine o número de pessoas que leem apenas um jornal.

(b) Quantas pessoas leem pelo menos dois jornais?

(c) Se I e III são jornais matutinos e II é um jornal vespertino, quantas pessoas leem pelo menos um jornal matutino mais um jornal vespertino?

(d) Quantas pessoas não leem nenhum jornal?

(e) Quantas pessoas leem apenas um jornal matutino e um jornal vespertino?

Passo 1

Vamos fazer o diagrama de venn novamente, já com os valores reais do quantitativo de habitantes:

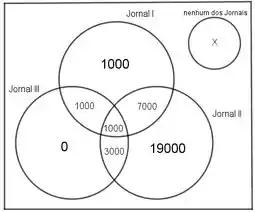
Vamos logo encontrar quanto é X, número de habitantes que não lê nenhum jornal:

Passo 2

a. Aqui basta olharmos do diagrama e fazer a soma:

Passo 3

b. Somando todos os valores no diagrama, exceto o X, temos?

Passo 4

c.

Passo 5

d.

Passo 6

e.

Resposta

a.

b.

c.

d.

e.